Informative Prior, the Conjugate
이번 포스트에선 unknown parameter $\theta$가 1차원일 때 자주 활용되는 대표적인 모델중에서 binomial model을 살펴보면서 만약 사전 정보가 충분한 경우 이를 기반으로 prior distribution을 설정할 때 고려해야 할 점들을 소개할 것이다.
2.1. Binomial Model
Binomial model은 주로 Bernoulli trials(베르누이 시행)을 따르는 연속적인 시행들을 분석할 때 활용한다. 각 시행은 어떤 알려지지 않은 확률로 발생하게 될텐데, binomial model은 그 확률을 추정하게 된다. 이 binomial이 실질적인 사회 문제에 적용되기엔 다소 거리감이 있겠지만, 이 모델은 그야말로 베이즈 이론의 시초였다.
데이터의 형태가 $n$회의 연속된 exchangeable Bernoulli trials이고, 각각은 ‘성공’ 혹은 ‘실패’로 나뉜다. 시행들이 서로 exchangeable하기 때문에 어느 회차에 성공했는지는 그닥 중요한 정보가 아니며, 우리는 데이터를 ‘전체 성공 횟수’로 요약할 수 있을 것이다. 이는, 만약 $\theta$를 population(모집단)에서 성공하는 비율(proportion)라고 둔다면, 우리의 데이터는 $\theta$를 parameter로 갖는 binomial distribution으로 설정할 수 있을 것이다. 그러므로 binomial model에서 sampling distribution은 다음과 같이 둘 수 있다.
\[p(y\vert \theta) = B(y\vert n, \theta)={n\choose y} \theta^y(1-\theta)^{n-y}\]베이지안 분석을 계속하기 위해서는 우리는 prior distribution $p(\theta)$에 대한 적절한 가정이 필요하다. 그래야만 우리는 full parameter model을 완성할 수 있기 때문이다. 하지만 prior distribution을 정하는 과정은 잠시 뒤에 알아보기로 하고 여기서는 간단하게 $\theta \sim \mathcal{U}(0, 1)$로 잡아보도록 하자. 즉, $p(\theta)\propto 1$이다. 그러면 posterior distribution은 다음과 같다.
\[p(\theta\vert y)\propto p(y\vert\theta)p(\theta) \propto \theta^y(1-\theta)^{n-y}\]Density의 꼴을 보았을 때 beta distribution임을 알 수 있다(물론 계수는 계산되지않는 unnormalized beta distribution이다). 즉,
\[\theta\vert y\sim \text{Beta}(y+1, n-y+1)\]이렇게 density가 계수를 포함한 전체 식으로 구하지 않아도, 어차피 계수는 density의 특징에 맞게 계산되므로 계수가 계산되지 않은 함수꼴만 보아도 우리는 분포를 유일하게 특정지을 수 있다.
Thomas Bayes는 사후, 1763년에 Essay towards Solving a Problem in the Doctorine of Chances에서 처음으로 inverse probability라는 개념을 사용하면서 binomial model을 소개했고, 이는 이후 베이즈 이론의 기틀을 다졌다. Inverse probability는 현재 posterior distribution에 준하는 개념이었는데, 그전까지는 단지 parameter $\theta$가 주어졌을 때 data $y$가 하나의 확률변수로써 가질 수 있는 값과 그 성질들을 연구하는 분위기였다면 베이즈는 이를 뒤집어(invert) 측정 데이터 $y$가 주어졌을 때 parameter $\theta$에 대한 결론 $\theta\vert y$을 확률의 언어로 도출했던 것이다. 논문에서는 ‘당구대’ 위의 공의 위치를 기반으로 과정을 제시했다.
- Prior distribution: 당구공 $W$이 당구대 위로 무작위로 던져졌다고 가정하자. 당구공의 위치 $\theta$는 전체 긴 모서리 길이에 대한 긴 모서리를 따라 왼쪽 끝에서부터 떨어져 있는 거리의 비율로 표현한다. 즉, 긴 모서리 길이를 1로 설정했을 때의 왼쪽 끝에서부터 긴 모서리를 따라 떨어진 거리를 $\theta$로 둔 것이다. 당구공 $W$이 각 위치에 떨어질 불확실성은 모두 동일하므로 $\theta$는 $\mathcal{U}(0, 1)$을 따른다고 가정했고, 이것이 prior distribution이 된다.
- Likelihood: 또다른 당구공 $O$가 무작위로 $n$번 던져졌다고 하자. $y$는 당구공 $O$가 당구공 $W$의 왼편에 떨어진 횟수라고 하자. 그러면 당구공 $W$는 이미 던져진 상황이므로 $\theta$는 주어졌다고 생각할 수 있다. 그 상황에서 $y$가 측정되는 것이므로 우리는 $y\vert \theta \sim B(n, \theta)$으로 모델을 설정할 수 있을 테고 이것이 곧 likelihood가 된다.
이러한 가정을 바탕으로 Bayes는 다음의 inverse probability를 얻을 수 있었다. 다음 식은 그가 논문에서 직접적으로 계산한 과정을 가져왔다.
\[\begin{align*} P(\theta\in(\theta_1, \theta_2)\vert y) &= \frac{P(\theta\in(\theta_1, \theta_2), y)}{p(y)} \\ &= \frac{\int_{\theta_1}^{\theta_2}p(y\vert \theta)p(\theta)\,d\theta}{p(y)} \\ &= \frac{\int_{\theta_1}^{\theta_2}{n\choose y}\theta^y(1-\theta)^{n-y}\,d\theta}{p(y)} \end{align*}\]Bayes는 분모 $p(y)$를 계산하는 데엔 성공했다.
\[\begin{align*} p(y) &= \int_0^1 {n\choose y}\theta^y(1-\theta)^{n-y}\,d\theta \\ &= {n\choose y}\frac{\Gamma(y+1)\Gamma(n-y+1)}{\Gamma(n+2)} \\ &= \frac{1}{n+1}, \quad y=0, \cdots, n \end{align*}\]이것이 한편으로 보여주는 것은, 데이터를 본격적으로 수집하기 전(=사전적으로, a priori)에는 $y$가 그 어떤 값으로 나올 확률이 동등하다는 것이다. Bayes는 한편 분자에 있는 식의 closed-form을 구하지 못했다. 실제로도 없기 때문에 값을 만약 구하고 싶으면 수치해법으로 접근해야 한다.
Laplace도 이와 비슷한 연구를 했다. Bayes가 이 연구를 하는지는 전혀 몰랐던 상태로 독립적으로 진행한 연구였다. 물론 당구대라는 동일한 물리적 상황을 두고 연구한 것은 아니었지만, 그는 출산 인구 중 여성의 비율을 알고자했다. 그도 우연치 않게 prior distribution을 $[0, 1]$ 위에서의 uniform distribution으로 가정했다. 당연하게도 동일한 결론식을 얻었으며, 분자에 있는 식을 계산하고자 노력한 흔적도 있었다. $\theta^y(1-\theta)^{n-y}$의 최댓값이 $\theta=y/n$에 있기 때문에 이를 기준으로 정규근사(normal approximation)를 하여 계산하였다. 1745년부터 1770년 사이 파리에서 출산한 인구 중 남성은 241,945명, 여성은 251,527명이었는데, Laplace가 이 데이터를 기반으로 베이지안 분석 기법으로 구한 posterior distribution에 의하면
\[P(\theta\ge 0.5\vert y=241,945, n=251,527+241,945)\approx 1.15\times 10^{-42}\]이었다. 이를 통해 그는 $\theta<0.5$임을 잠정적으로 확신했다.
이제 사후적으로(즉, 데이터가 측정이 되었을 때) 새로운 데이터에 대한 예측값을 알아보도록 하자. 즉, posterior prediction distribution을 구해보는 것이다. 우리는 이미 앞에서 Bayes에 의해 prior prediction distribution이
\[p(y) = \frac{1}{n+1}, \quad y=0, \cdots, n\]임을 밝혔다. 이제 직접 계산을 해보며 posterior prediction은 prior prediction과 비교했을 때 어떻게 달라지는지 그 변화를 살펴보자. $\tilde{y}$를 새로운 데이터라고 둘 때,
\[\begin{align*} P(\tilde{y}=1\vert y) &= \int_0^1 P(\tilde{y}\vert\theta, y)p(\theta\vert y)\,d\theta \\ &= \int_0^1 \theta p(\theta\vert y)\,d\theta \\ &= E[\theta\vert y] = \frac{y+1}{n+2} \end{align*}\]이 결과를 Laplace’s law of succession이라고 한다. 우리는 처음에 prior distribution을 uniform distribution으로 시작했고, 이를 바탕으로 도출한 prior prediction 또한 uniform한 형태를 띄었다($1/(n+1)$로 균등했으니 말이다). 하지만 데이터를 측정한 후, 우리는 성공횟수가 점점 더 많아지면 $P(\tilde{y}=1\vert y)$가 더 커지고, 사후적으로 성공할 확률이 증가한다는 결과를 얻을 수 있었다. 극단적으로 $y=n$일 때, 이 Laplace’s law는 다음 시행 때 성공 확률이 $(n+1)/(n+2)$임을 보여주고 있다. Laplace는 이 결과를 ‘내일 해가 뜰 확률은 얼마일까?’라는 질문에서 베이즈 접근법을 통해 해는 내일도 뜰 것이라는 결과를 보여주었다. 이 틀은 이후에 기본적인 시계열 모델의 얼개를 잡아주기도 한다.
2.2. Posterior Inference
베이지안 분석 기법을 binomial model를 예시로 구체적으로 어떤 방법으로 이루어지는지 알아보았다. 베이지안 추론은 prior distribution을 토대로 측정된 데이터를 거쳐서 posterior distribution에 도달한다. 미루어 짐작컨대, posterior distribution은 prior distribution과 데이터(혹은 likelihood)의 중간 지점에서 합치하여 나타날 것이다. 먼저 알 수 있는 것은, posterior distribution은 가장 불확실한 prior distribution에서 데이터에 의해 모집단의 정보가 더해지면서 posterior distribution은 그 불확실성이 줄어들 것이라는 점이다. 이는 수리적인 부분에서도 정확히 알 수 있다.
\[E\theta = EE[\theta\vert y]\]또,
\[Var(\theta) = E Var(\theta\vert y) + Var(E[\theta\vert y])\]먼저 iterating expectation property 혹은 smoothing이라고도 불리는 첫 번째 identity는 베이즈 분석의 시각으로 보았을 때 $\theta$의 prior mean은 가히 모든 가능한 posterior mean 값들의 sampling distribution 위에서 취해진 평균이다. 그 아래에 주어진 variance에 대한 identity는 앞서 설명했듯이 불확실성의 정도에 대해 설명한다. Posterior variance는 그 평균으로 보았을 때 prior variance보다 작으며, 그 작은 정도는 posterior mean 자체의 불확실성만큼이다. 이 Posterior mean 자체의 불확실성을 키움으로써, 우리는 $\theta$에 대한 불확실성을 사후에 줄일 수 있음을 앞으로 차차 살펴볼 것이다. 물론, 사후에 대한 불확실성은 그 평균(기댓값)으로 따졌기 때문에 특정 데이터에 대해서는 이 대소 관계가 성립하지 않을 수 있다.
Uniform distribution을 prior로 활용한 binomial model의 결과를 다시 참조해보자. Prior mean은 $1/2$, sampling distribution의 mean은 $y/n$, 그리고 posterior mean은 $(y+1)/(n+2)$임을 구했었다. 이들의 관계는 다음과 같이 설명될 수도 있다.
\[\frac{y+1}{n+2} = \frac{2}{n+2}\cdot\frac{1}{2} + \frac{n}{n+2}\cdot\frac{y}{n} = \gamma\cdot\frac{1}{2} + (1-\gamma)\cdot\frac{y}{n}\]즉, posterior mean은 prior mean과 sampling mean의 내분점 어딘가에서 합의를 이룸을 알 수 있다. 만약 데이터를 매우 많이 수집하여 데이터의 영향력을 키운다면, 즉 $n$을 무한히 키운다면 $\gamma$의 값은 0으로 수렴하게 되고 prior mean의 영향력은 0에 다가가게 된다. 그러므로 data의 영향력을 조절하기 좋은 수단 중 하나는 sample size을 조절하는 것이다.
이제 posterior distribution을 가지고 있을 때 통계학적인 추론을 어떻게 이어나갈 수 있을지 살펴보자. 기본적으로 posterior distribution은 $\theta$에 대해 현재 가지고 있는 모든 정보를 포함하고 있다고 생각하기 때문에 $\theta$에 대해 추론할 때는 posterior distribution으로 하는 것이 가장 정당할 것이다. 베이즈 추론에서는 그러므로 posterior distribution만을 이용하여 결과를 요약하고 추론하는데, 때문에 변수 변환을 복잡하게 취한 후거나 parameter가 다차원일 때도 유연하게 모델을 정립할 수 있다.
Posterior distribution 자체로는 뭔가 추론 결과를 제시하기보다는 다양한 방법을 통해 수치적으로 요약해야 할 것이다. 이때 활용하는 방법이 mean, median(중앙값), mode(최빈값), 혹은 나아가 standard deviation(표준편차), interquartile range(IQR) 등 고전적인 기술적 통계치를 사용하는 것이다.
또, 우리는 자연스럽게 confidence interval와 비슷한 개념을 가진 어떤 interval을 제시할 수도 있을 것이다. 베이즈 분석에서 제시하는 이런 interval들은 posterior distribution이 가지는 불확실성을 나타내는 데에 목적이 있다. 그래서 이들을 posterior (central) interval이라고 부른다. 그래서 $100(1-\alpha)$ posterior interval은 posterior distribution에서 가운데 $100(1-\alpha) \%$에 해당하는 interval, 즉 그 interval의 위나 아래가 $100(\alpha/2)\%$의확률을 가지는 interval이다.
조금 다른 방식으로 interval를 재구성할 수 있는데(interval이라는 표현보다는 region이 어울리겠지만), 이름하여 highest posterior density region이다. 비슷하게 이 interval 또한 $100(1-\alpha)\%$의 확률에 해당하는 값들을 포함하고 있는데, 대신 범위 안에 있는 값들은 범위 밖에 있는 값들보다 작지 아니하게 설정된다. 물론 느낌에도 highest posterior density region을 구하는 것이 수치적으로도 조금 더 까다롭겠지만, 대신에 posterior distribution에 대해 더 많은 정보를 포함하고 있을 것이다.
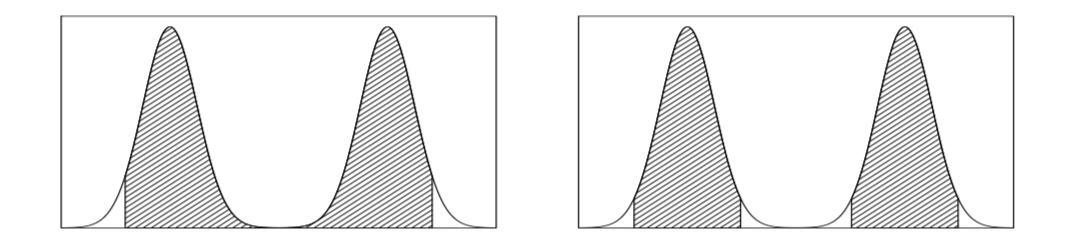
위에서 소개한 두 범위들은 만약 posterior distribution이 bimodal 모양을 가질 때(즉, 봉우리가 두 개인 모양) 그 차이가 조금이나마 나타난다. 아래 그림에서도 알 수 있듯이 왼쪽의 central interval은 가운데 쯤에 위치한 범위를 나타내고, highest posterior density region은 그 정의 탓에 가운데 부분에 포함되지 않은 부분이 있다. 그러므로 항상 interval의 형태를 띄는 것이 아닌 임의의 region으로 그 형태를 갖출 수도 있다. 만약 그 posterior distribution이 훨씬 많이 한 쪽으로 치우쳐져 있다면 두 범위는 더 극명한 차이를 보인다.
출처: Gelman, Bayesian Data Analysis, 3ed., 2020, Figure 2.2.
2.3. Informative Prior Distributions
지금까지 전체적인 베이즈 분석의 얼개를 살펴보았다면 이제는 다양한 상황에서 어떠한 철학적 근거를 바탕으로 유동적인 가정을 하며 베이즈적 접근을 시도해볼지 살펴보자. 처음으로 고려해볼 것은 prior distribution 설정에 관한 논의이다. 우리가 사전에 알고 있는 과학적 사실, 상식, 사전 연구 등을 활용하여 불확실성을 수치화한 prior distribution은 그 정형화된 설정 방식의 부재로 많은 논란이 되어왔다. 우리는 여기서 만약 정보가 충분하게 주어진 상황이라면 prior distribution을 어떻게 설정하면 될지를 시작으로 여러 다른 상황에서도 그 나름대로의 방법을 소개해보고자 한다.
먼저, prior distribution에 대한 베이즈적 해석을 구체적으로 개괄해보자. 먼저 population(모집단)의 관점에서 살펴보면, prior distribution은 취할 수 있는 모든 parameter의 값들을 모아 하나의 population을 표현하는 것이라고 볼 수 있다. Parameter는 사실 실질적 데이터는 아니므로 population의 실체가 따로 있진 않지만 또다른 관점으로는 사전지식의 정도(state of knowledge)를 표현한다고 볼 수 있는데, 만약 parameter를 prior distribution에서 무작위로 추출된다고 생각하면 사전 지식과 불확실성에 입각한 무작위 추출인 셈이다. 사실, 이런 철학적 관점을 뒤로하고 prior distribution을 현실을 모두 반영한 완벽한 무언가로 설계할 수 없는 것은 사실이다. 그러므로 우리가 prior distribution을 설정할 때는 조금 더 보수적으로 parameter가 그럴싸하게 될 것 같은 모든 값들을 모두 포함시키게 된다. 한편으로는 prior distribution이 굳이 parameter의 참값에 몰려있게 설정해도 그렇게 효용이 크지 않은데, 데이터를 실제로 수집할 때 이와 같은 유형의 prior distribution과 상당히 상이한 패턴으로 추출되는 경우가 많기 때문이다.
Bayes가 베이즈 분석으로 근간으로 제시한 binomial model를 앞서 소개했던 것을 다시 가져와보자. 별다른 설명 없이 prior distribution으로 uniform을 잡았던 것을 기억할 것이다. 하지만 베이즈 분석에 기반한 것이라면 prior distribution을 그렇게 설정한 것에 대한 정당성이 있어야 한다. Bayes가 직접 제시한 그 이유로는 그렇게 uniform prior로 잡은 후 도출한 prior predictive distribution 역시 ${0, 1, \cdots, n}$ 위의 uniform이었는데, 그가 실질적으로 보조실험을 통해 관측한 데이터도 역시 이를 따랐던 것이다. 물론 이것이 prior에 대한 직접적인 베이즈 철학을 담았다고 보긴 힘들지만 그나마 보조실험을 통해 prior를 그렇게 설정한 근거를 제시하려는 노력을 했다는 데엔 의의가 있다. 한편, Laplace가 제시한 이유는 거의 정당성이 없는 수준이었다. 하지만 그런 근거 없는 논리가 나중이 되어서는 오히려 parameter에 대해 아무런 정보가 없는 경우에 대해서 prior를 uniform을 설정하는 것이 적절하다는 principle of insufficient reason의 주창으로 이어진다. 우리는 이렇게 정보가 불충분한 경우에서도 방금 소개한 principle과 더불어 prior를 설정하는 몇 가지 관행들을 아래에서 소개할 것이다.
Binomial model를 계속해서 살펴보자. 우리는 앞서 likelihood가 다음과 같은 꼴로 주어짐을 알았다(앞으로의 논리 전개를 위해 likelihood라고 표현하면서 일부러 $\theta$에 대한 함수로 취급하고 $y$에 대한 표현은 상수 취급 했다).
\[p(y\vert\theta) \propto \theta^a (1-\theta)^b\]그러므로, 수학적으로 계산하기 편리하려면 일반적으로 prior distribution도 likelihood과 같은 꼴을 가지도록 설정하는 방법을 고안할 수 있다. 즉, parameter $\alpha$와 $\beta$에 대하여 prior density를 다음과 같이 두자.
\[p(\theta)\propto \theta^{\alpha-1}(1-\theta)^{\beta-1}\]먼저 눈치를 챘을지 모르겠지만, 이는 unnormalized된 $\text{Beta}(\alpha, \beta)$의 density이다. 이 prior가 담고 있는 의미로는 사전에 $(\alpha-1)$번 성공할 때 $(\beta-1)$번 실패한 기록이 있다는 것으로 붙일 수 있다. 이렇게 prior distribution에 다시금 parameter가 생기는 경우가 많은데, 이런 parameter를 hyperparameter라고 부른다. 물론 이 hyperparameter들 또한 적절한 값으로 선택되어야 하며, 그 방법들은 여러가지가 있다. 사전에 진행하는 실험으로(이를 empirical Bayes라고 표현하기도 한다) 정보를 얻는 방식이 있는 한편, 모델 구조를 확장하여 hyperparameter들 또한 어떤 초월적인 prior distribution을 따른다는 hierarchical Bayes model로 접근하기도 한다.
하여튼, 이 방식들은 나중에 다루어보는 것으로 하고 당분간은 이 hyperparameter들은 적절한 값으로 이미 선택되었다고 가정할 것이다. 그러면 우리는 다음의 posterior distribution을 얻을 수 있다.
\[\begin{align*} p(\theta\vert y)&\propto p(y\vert\theta)p(\theta) \\ &= \theta^{y+\alpha-1}(1-\theta)^{n-y+\beta-1} \end{align*}\]이는 $\text{Beta}(\alpha+y, \beta+n-y)$의 density임을 알 수 있다. 이처럼 posterior distribution이 prior distribution과 같은 꼴로 나타나는 성질을 conjugacy라고 한다. 여기서 Beta distribution은 binomial likelihood에 대하여 conjugate family가 될 수 있다. 조금 더 수학적으로 정의한다면, $\mathcal{F}$를 sampling distribution $p(y\vert \theta)$가 속해 있는 class라고 정의하고, $\mathcal{P}$를 parameter $\theta$의 prior distribution들의 class라고 정의하자. 그러면 만약
\[p(\theta\vert y)\in \mathcal{P}, \quad \forall p(\cdot\vert\theta)\in\mathcal{F} \quad\text{and} \quad \forall p(\cdot)\in\mathcal{P}\]를 만족하면 class $\mathcal{P}$는 $\mathcal{F}$에 대하여 conjugate라고 말한다. 다만 $\mathcal{P}$를 그저 모든 distribution의 class로 놓게 되면, $\mathcal{P}$는 그 어떤 경우에 대해서도 위 조건을 성립시키므로 conjugate가 되므로 이 정의가 모호한 점은 있다. 하지만 우리가 진정으로 관심있는 것은 가장 자연스러운 $\mathcal{P}$일 것이며, 이는 보통 likelihood의 함수 형태를 따와 꼴을 결정하는 식으로 이루어지게 된다.
Conjugate family는 수학적으로 간편함을 가지고 있는데, posterior distribution의 꼴을 이미 알고 있으므로 구체적으로 그 density를 계산해보지 않고 그 distribution의 parameter만 계산해도 온전히 알 수 있다는 점에서 그러하다. 그러나 우리가 알고 있는 정보가 conjugate family와 반한다면 조금 불편하더라도 그 정보를 기반한 prior distribution을 쓰는 편이 낫다.
우리가 방금 구한 posterior distribution을 기반으로 추론을 조금 해보자. 먼저 posterior mean, 즉 미래에 추가로 시행을 할 때의 기대되는 사후 확률은
\[E[\theta\vert y] = \frac{\alpha+y}{\alpha+\beta+n}\]인데, 이는 항상 표본 성공 비율 $y/n$과 prior mean $\alpha/(\alpha+\beta)$ 사이에 값이 놓임을 알 수 있다. 나아가 posterior variance는
\[Var(\theta\vert y) = \frac{(\alpha+y)(\beta+n-y)}{(\alpha+\beta+n)^2(\alpha+\beta+n+1)} = \frac{E[\theta\vert y](1-E[\theta\vert y])}{\alpha+\beta+n-1}\]로 주어진다. 만약 고정된 $\alpha$와 $\beta$에 대하여 $y$와 $n-y$가 매우 커진다면 $E[\theta\vert y]\approx y/n$, $Var(\theta\vert y)\approx \frac{1}{n}\frac{y}{n}\left(1-\frac{y}{n}\right)$로 근사된다. 즉 모두 $1/n$의 속도로 0으로 수렴하는 형태를 가진다. 이로써 sample size가 커지면 데이터의 영향이 막대해지고 prior distribution의 영향은 0으로 수렴하게 된다. 이에 힘입어 우리는 이후에 빈도론적 접근에서 중요시하는 sample size가 극한으로 가는 상황, 여기서 비롯되는 central limit theorem(중심극한정리) 같은 성질들을 베이즈 분석에서도 적용하여 매우 흡사한 결론을 도출할 수 있음을 살펴볼 것이다. 이를테면,
\[\left(\left.\frac{\theta-E[\theta\vert y]}{\sqrt{Var(\theta\vert y)}}\right\vert y\right)\to N(0, 1)\]이는 이후에 분석하기 다소 난해한 posterior distribution에 대해서도 normal distribution으로의 근사를 통해 수월한 사후 추론을 진행할 수 있다.
조금 더 일반적으로 likelihood가 exponential family에 속하는 경우, 혹은 위의conjugacy 정의에 활용했던 표현을 빌려 만약 $\mathcal{F}$가 exponential family인 경우를 살펴보자. 그러면 이에 속하는 sample distribution은 다음과 같은 꼴을 가질 것이다.
\[p(y_i\vert \theta) = A(y_i)h(\theta)\exp[\eta(\theta)^T T(y_i)]\]이때 $\eta(\theta), T(y_u)\in\mathbb{R}^n$는 벡터 형태이다. $n$개의 sample을 독립적으로 추출하여 데이터를 추출하면 sequence $y=(y_1, \cdots, y_n)$를 구성할 수 있고, 이의 likelihood는
\[p(y\vert \theta) = \left(\prod_{i=1}^n A(y_i)\right)[h(\theta)]^n \exp\left[\eta(\theta)^T\sum_{i=1}^n T(y_i)\right]\]로 주어진다. 즉, 간단하게 likelihood는 다음과 같은 꼴을 가진다고 표현할 수 있다.
\[p(y\vert \theta)\propto [h(\theta)]^n e^{\eta(\theta)^T T(y)}, \quad\text{where}\quad T(y)=\sum_{i=1}^n T(y_i)\]수리통계에서 알 수 있겠지만 $T(y)$는 여기서 $\theta$의 sufficient statistic이다. 베이즈 분석에서도 역시 sufficient statistic이 유용한데, likelihood와 posterior distribution을 수식적으로 정립하는데 많은 도움을 준다. 아무쪼록, 만약 prior density를 다음과 같이 설정한다면
\[p(\theta)\propto [h(\theta)]^{\varphi} e^{\eta(\theta)^T\nu}\]posterior density는 다음과 같이 쉽게 구할 수 있다.
\[p(\theta\vert y)\propto g(\theta)^{\varphi + n}e^{\eta(\theta)^T(\nu + T(y))}\]그러므로 위에서 설정한 prior density는 conjugate함을 알 수 있다. 신기한 사실은 exponential family만이 이러한 자연스러운 conjugate prior distribution이 있는 class임이 증명되어 있다. 그 이유로 한 몫 하는 것은 모든 sample size $n$에 대하여 sufficient statistics가 한정적인 개수로 주어지는 경우는 exponential type밖에 없기 때문이다.
다음 포스트에서는 정보가 충분하지 않을 때 prior distribution을 설정하는 여러 방법론들을 살펴볼 것이다. 그러기 위해서는 먼저 likelihood가 normal distribution을 따를 때의 베이즈 분석 기법들을 익힘으로써 우리가 다룰 수 있는 예시가 많아져야 한다. Normal distribution은 parameter가 $\mu$와 $\sigma^2$ 총 두 개가 있지만, 다음 포스트에서 소개하는 모델들은 둘 중 하나는 알고 있는 상태에서 다른 것을 추론하는 것들이다. 물론 두 개를 동시에 추론할 수도 있지만, 이는 prior distribution에 관한 논의들이 끝난 후 다루도록 하겠다.