2-3. The Fundamental Law of Active Management, The Statistical Issues in QEPM
2. The Fundamentals of QEPM
Tenets 3&4: The Fundamental Law, The Information Criterion, and QEPM
- Quantitative analysis creates statistical arbitrage opportunities. 정량적 분석가는 통계적 차익거래의 기회를 만들어낸다.
- Quantitative analysis combines all the available information in an efficient way. 정량적 분석가는 효율적인 방법으로 존재하는 정보를 모두 조합한다.
이 두 tenet은 fundamental law of active management의 틀에 기초한다. 이 fundamental law는 간단하면서도 PM이 portfolio을 구성하는 데 관여한 부분을 직관적으로 나타낸다. QEPM에서 목표 중 하나로 IR(information ratio) 극대화가 있었는데, fundamental law는 통계적인 방법과 관련 정보로 얻을 수 있는 효율성으로 이를 최적화하는 방법을 이해할 수 있도록 도와준다.
Fundamental law에 의하면 IR은 information coefficient(IC)와 breadth(BR)의 제곱근의 곱으로 이루어진다. 즉,
\[IR= IC \cdot \sqrt{BR}\]가 성립한다. IR의 정의에 따라서 우리는
\[\frac{\alpha^B}{w} = IC\cdot\sqrt{BR}\]로도 표현할 수 있다. IC는 기존 모델에 있던 변수보다 더 유의한 인자를 찾으면 증가한다. BR은 기존 모델에 있던 변수와 상관관계가 없는 인자를 찾을 수록 증가한다.
Fundamental law는 정량적 portfolio management의 과정에 더 넓은 숲을 보기 위하여 제안되었다. 하지만 가끔 이 법칙이 QEPM을 위한 직접적인 도구로 취급하고 이를 활용하여 portfolio를 직접 구성하려는 등 그 역할에 오해를 사는 경우가 있다. Fundamental law는 QEPM을 전반적으로 이해할 수 있는 도구로써 QEPM 분석을 위해 개념적인 틀을 제공할 뿐이다.
The Truth about the Fundamental Law
QEPM의 주 기능 중 하나는 주식의 수익률과 설명 변수들 간의 관계를 규명하여 적합한 모델을 추정하고, 이를 통해 미래 수익률을 예측하는 데에 있다. 이를테면, 각 시간 $t$마다 주식 $i$의 수익률 $r_{it}$를 $K$개의 인자 프리미엄 $f_{1t}, \cdots, f_{Kt}$의 선형함수라고 가정하는 모델을 고려하자.
\[r_{it} =\alpha_i + \beta_{i1}f_{1t}+\cdots + \beta_{iK}f_{Kt}+\epsilon_{it}\]이때 $\alpha_i$와 $\beta_{i1}, \cdots, \beta_{iK}$는 추정되어야 할 변수이고 $\epsilon_{it}$는 오차를 나타내는 확률 변수이다. Fundamental law가 이 상황에서 설명하는 것은 얼마나 이 모델이 주식 수익률을 잘 설명하는지, 모델의 gooness of fit을 평가한다고 볼 수 있다. IR의 공식에 따르면, 모델의 goodness of fit은 설명 변수의 개수와 각 변수가 제공하는 평균 기여도를 곱한 값이다. Fundamental law은 물론 이런 형식 말고도 여러 다른 표현 방식이 있지만, 결국은 다음의 틀 안에서 움직인다.
- $IR^2$은 미래 수익률 예측 모델의 goodness of fit($R^2$)로 근사할 수 있다.
- Breadth는 미래 수익률 예측 모델의 설명 변수의 개수와 같다.
- $IC^2$는 $R^2$을 증가시키는 각 설명변수의 평균적인 기여도와 같다.
- Fundamental law는 goodness of fit을 설명변수의 개수와 각 설명변수의 평균적인 기여도로 분해할 수 있음을 보여준다.
- BK가 무시되고 무위험자산 수익률이 portfolio 수익률에서 제하였다면, $IR$은 결국 모델이 얻을 수 있는 Sharpe ratio의 최대값이다. 그리고 fundamental law는 Sharpe ratio의 최대값을 설명변수의 개수와 그들의 평균적인 기여도로 분해한다.
The Information Criterion
Fundamental law의 또다른 오해는 이 법칙이 모든 active한 portfolio management에 적용되는 건줄 안다는 것이다. Fundamental law는 오로지 PM이 optimal한 portfolio를 제작했을 때만 성립한다. 하지만 많은 경우에 있어서 PM은 suboptimal한 portfolio를 만들기 마련인데, 그 이유로 존재하는 모든 정보를 가장 효율적인 방법으로 사용하지 못했기 때문, 즉 tenet 4를 위반했기 때문이 크다. 이는 다음과 같이 the information criterion으로 정해둔 바, active management에서 가장 일반적인 원리가 된다.
Lemma 1 (The Information Criterion) Active portfolio management에서 fundamental law로써 표현했던 $IR = IC\cdot\sqrt{BR}$는 PM이 존재하는 모든 정보를 가장 효율적인 방법으로 조합했을 때만 유효하다.
이를테면 PM이 애널리스트 등급(analyst ratings)이 직전 월보다 좋아진 주식을 가지고 동등한 비율로 구성하여 portfolio를 만들었다고 하자. Portfolio에 반영되는 것들을 요인으로 찾아 변수로 둘 수 있을 것이다. 즉, 여기에서는 $\beta_{it}$를 정의하여, 만약 $i$번째 주식의 등급이 시간 $t$에서보다 $t+1$에서 향상되었다면 $\beta_{it}=1$, 그렇지 않은 경우에는 $\beta_{it}=0$의 값을 갖는 것이다. 그러면 PM은 과거의 데이터를 통해 다음의 식을 만족하는 모델을 추정하게 된다.
\(r_{i, t+1} = \alpha + \beta_{it}f + \epsilon_{i, t+1}\) 여기서 $\alpha$와 $f$는 추정해야 하는 변수가 된다. 만약 추정한 $f$가 양수라면 $\beta_{it}=1$을 갖는 주식이 더 높은 미래 수익률을 얻는다. 따라서 PM은 $\beta_{it}=1$인 주식만을 모아 동등한 비율로 portfolio을 만드는 것이다.
하지만, PM은 여기에서 존재하는 모든 정보를 활용하지 않았다. 위 모델에서 제시하는 것이 단지 $\beta_{it}=1$을 만족하는 주식이 높은 기대 수익률을 가진다는 것뿐만이 아니라, 어떤 주식이 더 높은 위험, 혹은 volatility를 갖는지도 보여준다. 그리고 이렇게 알게 된 각 주식마다의 위험도는 각 주식을 어느 비중으로 하여 portfolio를 구성해야 할지를 알려줄텐데, 위에서는 그냥 동등한 비율로 portfolio를 구성했다. 궁극적으로 PM은 information criterion을 만족하지 않는 porfolio를 구성했다. 이 lemma가 성립하지 않는다는 것은 달리 말하여 분명 더 좋게 portfolio를 구성할 수 있는 방법이 있다는 것이다.
Information Loss
정보의 손실은 fundamental law의 틀 아래에서 손쉽게 수치화할 수 있다. IR의 역할은 PM이 얼마나 기여했는지, 즉 PM이 portfolio의 수익률을 증진시키기 위해 활용한 정보가 얼마나 기여했는지를 알려준다. 조금 다른 시각으로 바라보면 IR은 PM이 얼마나 덜 기여했는지도 알려주기도 한다. 모든 정보를 최대한 효율적으로 활용하면 IR이 극대화될 텐데, 그중 일부의 정보만 활용하여 얻은 IR은 극대값의 IR과의 차이를 통해 정보가 얼마나 손실되었는지 알 수 있다. 즉, information loss(IL)은 다음과 같다.
\[IL = \text{maximum}\, IR - \text{actual}\, IR\]위에서 소개한 IR이 Sharpe ratio의 최대값으로 근사될 수 있다는 점에서 미루어보아 IR은 reward-to-risk(위험 대비 보상) 비율로도 볼 수 있다. 그러므로 만약 IR이 0.1의 값을 가진다면, 매 10%의 위험마다 1%의 잠재적 추가 수익률을 놓치고 있다고 볼 수 있다.
Tenets 5, 6, and 7: Statistical Issues in QEPM
- Quantitative models should be based on sound economic theories. 정량적 모델들은 전체적으로 적용되는 경제적 이론을 기초로 하여야 한다.
- Quantitative models should reflect persistent and stable patterns. 정랼적 모델들은 (불규칙한 데이터를 반영하기보다) 지속적이고 안정적인 패턴들을 반영해야 한다.
- Deviations of a portfolio from the benchmark are justified only if the uncertainty is small enough. Benchmark로부터 오는 portfolio의 분산은 (모델 추정 할 때의) 불확실성이 충분이 작을 때만 정당화된다.
PM로서 절대 무시해선 안 되는, 그러나 간과하기 쉬운 세 가지 유의할 점이 있다. 데이터 마이닝(data mining), 변수 안정성(parameter stability, 그리고 변수 불확실성(parameter uncertainty)이다.
Data Mining
정량적 PM이 마주하는 가장 큰 과제 중 하나는 data mining를 피하는 것이다. 이는 Tenet 5번을 위배한다. 하지만 문제는 막상 모델을 구성하고 분석할 때 data mining의 이슈를 탐지하기 쉽지 않다는 것이다.
Data mining(데이터로부터 결론 도출)은 과거 주식 수익률을 바탕으로 회귀 모델을 만들 때 너무 많은 요인의 조합으로 만들고 나서, 그중 한 변수가 주식의 수익률과 큰 상관관계가 있다고 주장하지만 실은 아무 의미 없는 경우를 말한다. 예컨대, 주식의 수익률을 잘 설명할 것 같은 99개의 변수 $f_1, \cdots, f_{99}$를 고려하자. $t$번째 달에서의 주식의 수익률을 $r_t$, 각 요인들의 값을 $f_{1t}, \cdots, f_{99t}$라고 하면, 우리는 다음의 모델을 만들어 변수를 적절히 추정하면 된다.
\[r_t = \alpha + \beta_1f_{1t}+\cdots +\beta_{99}f_{99t}+\epsilon_t, \quad t = 1, \cdots, 100\]100달치의 주식 수익률 데이터를 관측했다고 가정하고 이를 바탕으로 모델을 추정했을 때, goodness of fit은 $R^2 = 1$이 도출될 것이다. 100달치의 데이터를 활용하여 100개의 모수를 추정하였으므로 error가 0이 되기 때문이다. 하지만 이것이 모델을 잘 만들었다는 방증이 되지 않으며, 여기서 모델이 유효한지 검정할 아무런 통계적 추론을 할 수가 없다.
Data mining의 문제가 이렇게 대놓고 주어지지 않는 경우가 훨씬 많다. 유의한 변수를 추출하기 위하여 stepwise 회귀를 거친다고 하자. 이러한 회귀 분석에서 우리는 모델이 적합한지 통계적 추론을 통해 검정할 수 있을까? 어렵다. 이를테면, 100개의 각 요인의 값을 무작위로 뽑은 숫자로 설정해보기로 한다. 그리고 나서 요인들 중에서 어떻게든 유의한 변수를 추출한다면, 워낙 많은 변수들로부터 골라내는 것이므로 유의한 변수야 분명히 도출되긴 할 것이다. 우리가 회귀를 설정한 그 목적서부터 유의미한 변수를추출하기 위함이고, 어떤 변수가 선택되든 간에 결국 선택된 것들은 ‘유의하다’고 할 터다. 그러므로 그 변수가 진짜로 주식 수익률을 잘 설명한다고 말할 근거가 명확하지 않은 것이다.
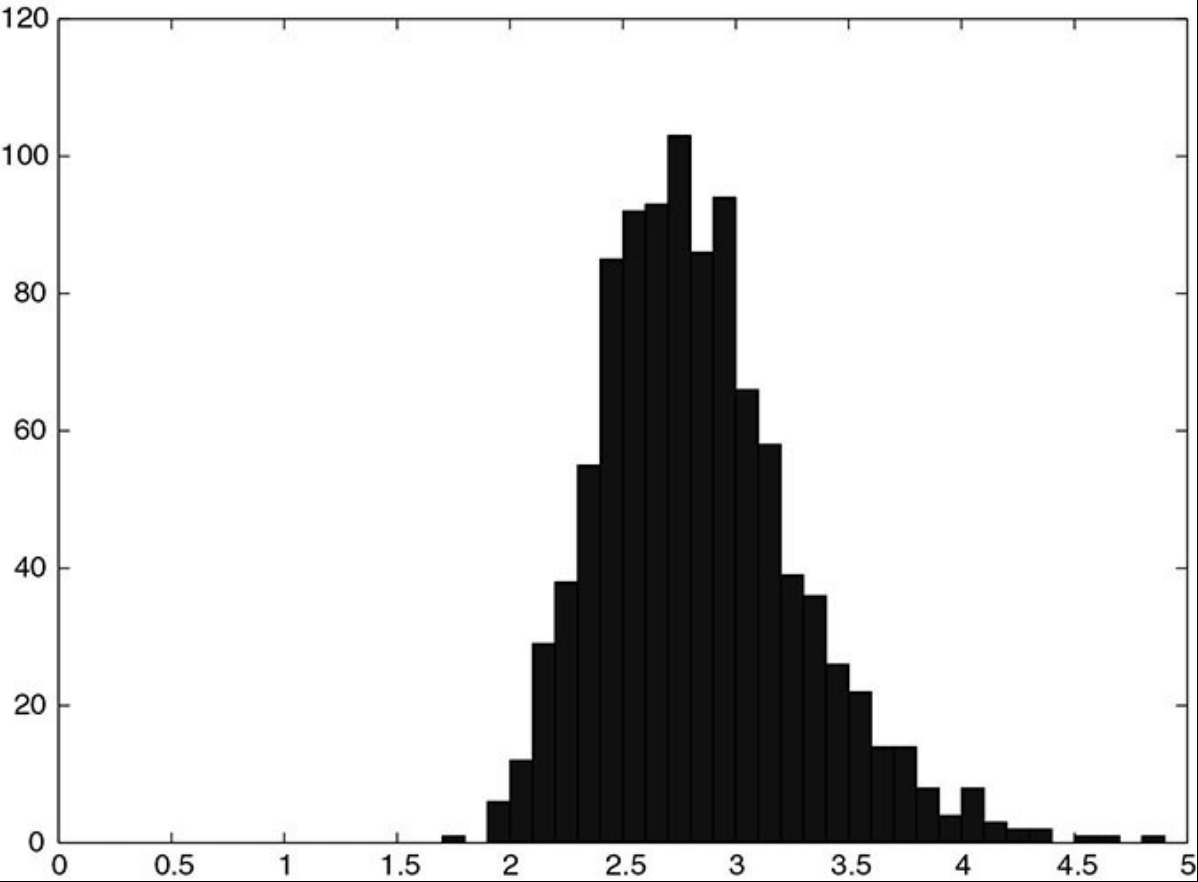
이를 더 명확하게 볼 수 있는 시뮬레이션 하나를 구축할 수 있다. 위에서 했던 것과 마찬가지로, 100개의 관측치와 100개의 설명 변수 모두 표준정규분포에서 독립적으로 추출했다고 하자. 그리고 stepwise 회귀 분석을 통해 가장 유의한 변수를 추출하고, 그 변수의 유의성을 보여주는 $t$-statistic의 절댓값을 기록해보는 것이다. 이 시뮬레이션을 1000번 반복하여 얻은 $t$-statistic들에 대한 분포도는 예를 들어 다음과 같다.
대부분 유의하다라고 말할 수 있는 수준인 2를 넘어섬을 알 수 있다. 하지만 시뮬레이션 디자인 단계부터 그렇게 의도했듯이 설명변수는 종속변수와 아무런 관련이 없다. $t$-statistic이 단지 높다는 이유로 모델 자체의 $R^2$ 값 또한 높을 텐데, 여기서 $R^2$의 값은 무의미해진다.
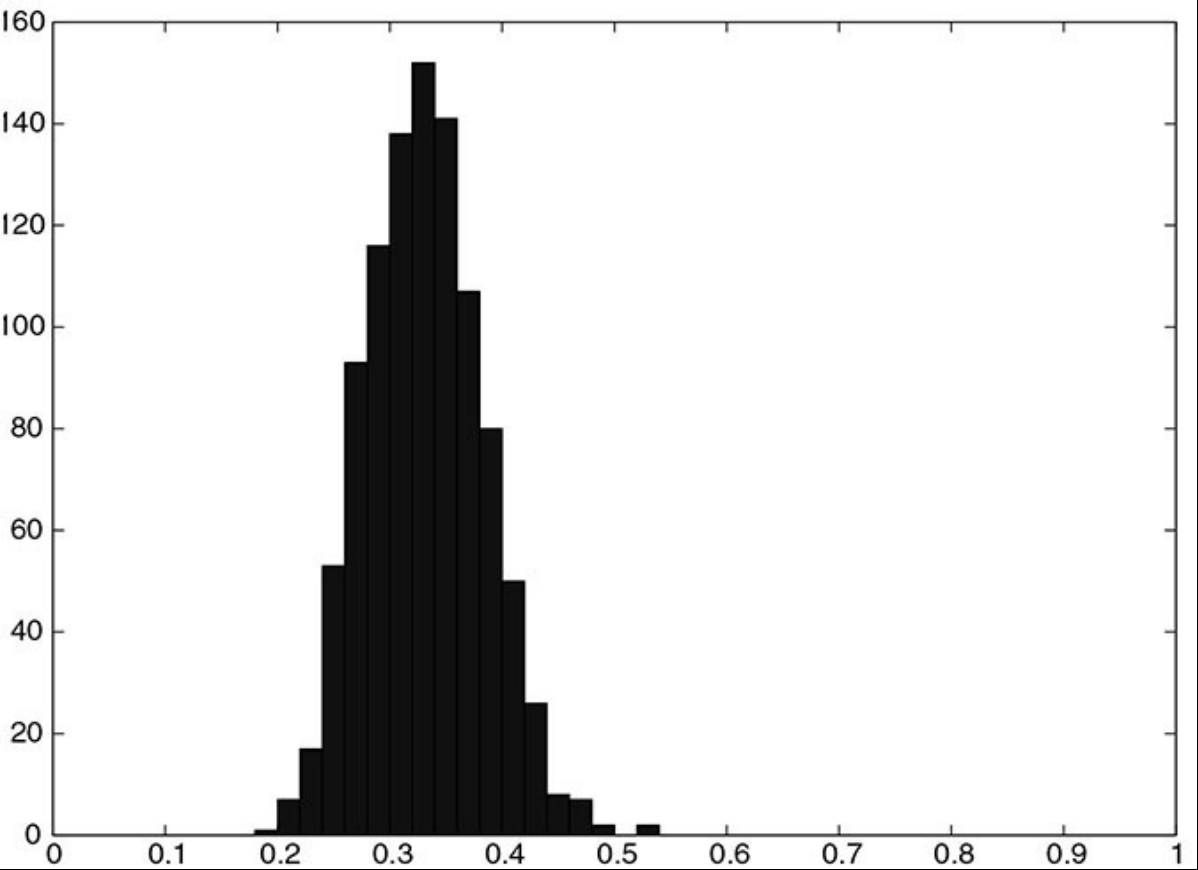
아까의 실험에서 이젠 가장 유의한 10개의 설명변수를 추출하여 그들끼리 다시 회귀분석을 통해 $R^2$의 값을 추출했다. 이 역시 1000번 반복하면 $R^2$ 값에 대한 분포는 다음과 같이 대부분 0.3에서 0.4 사이에 집중되는 것을 알 수 있다. 이는 사회적인 데이터를 바탕으로 회귀분석을 시도하였을 때 꽤 높은 적합성에 해당하는 값이다. 하지만 $R^2$는 여기에서도 실질적인 통계적 유의성을 의미하지 않는다.
이처럼 PM이 의도로 조작하지 않아도 우리는 통계적인 사유에 근거하지 않아도 겉보기엔 유의한 결과를 얻은 것처럼 보이는 결과를 가질 수도 있다. 혹은 통계적 결론으로 도출한 것들이 data mining 문제 탓에 오명을 가져올 수도 있게 된다. 이런 data mining은 학계에서 심심치 않게 발생한다. 어떤 한 연구자가 주식 수익률에 유의하게 영향을 주는 한 변수를 주장하고 이것이 유명세를 타 모두에게 지지를 받는 한편 다른 연구 결과들도 분명 그들만이 주장하는 유의한 변수가 있을 텐데도 주목받지 못할 때, 이 연구자 집단은 그 연구자의 결과를 바탕으로 다시 모델을 새우게 되고 또 편향된 결론을 얻어가며, 결국은 존재하지도 않는 패턴을 발견했다고 주장하는 일종의 전체적인 data mining, 혹은 data snooping이라고 일컫는 것에 말려들 수 있다.
어떤 한 유의한 변수를 추출하고 검정할 때 data mining 혹은 data snooping을 완전히 배제하고서 할 수는 없는 노릇이다. 그렇게 할 수 있으려면 우리가 살펴보는 데이터가 그 어느 연구자도 그 변수를 검정하려고 사용해본 데이터가 아닌 완전히 새롭고 신선한 데이터야 한다. 만약 사용하는 데이터가 이미 다른 연구에서 활용되었다면 우리의 결론이 그들의 결론에 영향받을지도 모르기 때문이다. 일례로 이미 익히 알려진 P/E ratio에 따른 anomaly는 우리만의 회귀 분석을 통해 유의성을 검정하여도, 그 누구에게도 사용되지 않은 데이터를 활용하지 않는 이상 P/E ratio라는 변수를 가지고 통계적 유의성 검정을 하지 못한다.
이를 방지하기 가장 좋은 수단으로 제안된 것이 tenet 5, 즉 모든 모델은 상식과 익히 알려진 건전한 경제 이론을 활용하는 것이다. 실험적으로 제안된 증거만으로는 실질적 판단을 내리기엔 충분하지 않은 근거의 기반이 될 수 있다. 모델 또한 아무 요인을 다 집어넣는 것이 아닌, 이 요인이 주식 수익률에 영향을 미치는 정당한 이유, 그 이유 중에서도 다른 연구자에게 이미 제안되지 않은 새로운 근거 아래에서 고려되어야 한다.
Data mining을 피할 수 있는 이런 이론적 방향에 더불어, 얼마든지 이를 피할 수 있는 다른 방법들이 있다. 이를테면, 이전 연구자들이 anoamly를 계속 밝혀내는 과정 속에서 제안하는 data snooping을 조절하는 방법으로는 고려하는 요인들 혹은 투자 전략에 Bayesian adjustment와 같은 통계 테크닉들을 활용하는 방법과, 시행하는 검정의 횟수(혹은 심지어는 이미 이전에 시행된 검정의 횟수와 그중 현재 연구자의 믿음에 영향을 미친 검정 횟수)에 기반한 수정된 $p$-value와 $t$-statistic을 활용하는 방법이 있다.
Parameter Stability
과거 데이터를 기반으로 미래를 예측한다면, 과거는 스스로 반복한다는 것을 가정해야 말이 될 것이다. 하지만 시장의 끊임없는 변동성은 이러한 규칙적인 과거 패턴들을 해치기 마련이다. 이를테면 CAPM을 통해 추정한 $\beta$가 있다면, 이 값이 차기에도 같은 수준을 유지할 것인지 중요할 것이다. 이는 더욱이 복잡한 모델에서도 궁극적으로 도달하는 물음을 살펴보아야, 즉 추정한 변수가 시간에 따라 안정적일지 따져야 할 것이다.
모수의 안정성을 고려하는 결국 데이터의 표본 크기를 결정하는데 아주 중요한 역할을 한다. 가령, CAPM에서 추정한 $\beta$가 일반적으로 5년 이상 일정 수준을 유지하지 못한다고 했을 때, 우리는 모델의 추정 과정을 거칠 때 5년 이상의 데이터는 넣으면 안 된다. 이에 대한 논의는 chapter 16에서 더 자세히 다룰 것이다.
지난 수 년동안 변수의 안정성을 위협하는 요인들이 정말 많아졌다. 당연하게도 이에 따른 정량석 투자의 위험도 또한 덩달아 증가하였다. 이는 부분적으로는 이전에도 언급하였던 anomaly인 crowding 현상이 동반되기 때문이다. 이로써 사람들이 똑같은 전략에 똑같은 거래를 하여 시장의 유동성이 줄어들었으며, 수익률과 위험도 사이의 역학적 관계가 변화되었다. 그러므로 PM은 새로운 변수를 색출하고자 노력하고, 그럼으로써 유명해진 전략들은 그 유명도 자체로 미래 예측력을 감소시킬 수 있을 것이다. 미래 예측력을 제대로 평가하기 위해서는 이와 같은 이유로 거래 비용까지 고려하는 등 실질적인 backtesting을 거쳐야 하며, crowding 현상을 염두에 두고, 변수 자체가 시간에 따라 어떻게 자연스럽게 변하는지도 관찰하는 것이 좋다.
Parameter Uncertainty
추가 정보를 아는 것은 나쁠 것이 전혀 없고, 오히려 도움이 되는 경우가 많다. 하지만 추가 정보다 항상 portfolio의 구성을 바꾸는 것은 아니다. Active한 PM이 그가 구성한 porfolio가 초과 수익률을 가져다준다고 해도, 해당 portfolio은 너무 과한 위험도를 수반하고 있을 수 있다. 그리고 그 위험도는 정량적으로 측덩될 수 있다.
Portfolio의 위험도가 수면 위에 올라와있지 않아도, 모수의 불확실성이 굉장히 높은 수준일 수 있으며 이 또한 위험도에 반영된다. 통계적 추정을 했다면 추정에는 오차를 수반하기 때문에 어느 정도의 불확실성을 가지고 있을 수 있고, 이는 standard error라는 이름으로 측정이 된다. Portfolio 구성 시 가장 기본이 되는 mean-variance 최적화 과정도 portfolio의 위험도로 이러한 standard error를 고려한다.
Standard error는 모수의 추정에서 나타나는 오차로써 두 가지에만 영향을 받는다. (1) 첫째로는 모델 오차의 variance에, (2) 둘째로는 설명변수의 variance에 영향받는다. 첫째로 소개한 variance는 모델이 얼마나 정밀(precise)한지 나타낸다. 그리고 후자로 설명한 variance는 얼마나 데이터가 정보를 제공하는지를 설명한다(피셔 정보 관련한 설명으로 이해하면 될 듯). 그러므로 만약 이 후자의 variance가 0이라면, 데이터가 가져다주는 정보는 없기에 standard error은 무한히 커지게 될 것이다. PM은 모수의 추정값뿐만 아니라 추정량(estimator)의 standard error의 추정치 또한 고려해야 한다. Standard error의 추정치가 크다면 이는 분명히 portfolio의 위험도에 그대로 반영될 것이기 때문이다. 이는 추후 portfolio의 선택 이론에 활용되는 Bayesian econometrics의 발단이 되며, chapter 14에서 자세히 다룰 것이다.