Paper Review: Memory Networks

• Weston, J., Chopra, S., & Bordes, A. (2014). Memory networks. arXiv preprint arXiv:1410.3916.
• Sukhbaatar, S., Weston, J., & Fergus, R. (2015). End-to-end memory networks. Advances in neural information processing systems, 28.
• Kumar, A., Irsoy, O., Ondruska, P., Iyyer, M., Bradbury, J., Gulrajani, I., … & Socher, R. (2016, June). Ask me anything: Dynamic memory networks for natural language processing. In International conference on machine learning (pp. 1378-1387). PMLR.

Intro

직전 리뷰에서 소개하였듯, RNN이나 LSTM으로 이루어진 encoder-decoder 구조가 결국 final state에서 만들어진 고정된 크기의 context vector만으로 정보 전달하는 탓에 긴 문장에 대해서는 성능 저하가 극심했는데, attention을 통해서 각 stage에 입력되는 정보를 필요에 따라 선택(집중할 것에 집중하고, 덜 집중할 것에 덜 집중하는 식으로)하여 전달할 수 있게 되었으므로 정보 전달에 대한 기존 문제가 해결되었고, 때문에 점점 주목받는 기법이 되었다. 하지만 Transformer가 “Attention is all you need”(Ashish et al., 2017)라는 논문을 통해서 탄생하기까지는 attention에 대한 더 발전된 논의가 있었기에 가능했다. 그러므로 attention과 관련하여 조금 더 살펴볼 것들이 있는데, 바로 다음과 같다.

• Recurrent attention mechanism(-> memory network): 기존에는 각 stage마다 입력되는 단어들에 대해서 RNN 등을 계속 반복하여 처리를 한 후 attention을 적용했다면(sequence-aligned recurrence), attention만을 반복하여 처리하는 모델.
• Inter-attention(-> Cross-attention)과 Intra-attention(-> Self-attention)의 아이디어, 각각의 용도.

각각에 대해서 논문 리뷰를 할 예정인데, 그 시작으로 memory를 활용하여 attention의 효과를 극대화한 세 가지의 논문을 차례로 리뷰하고자 한다.

• Weston, J., Chopra, S., & Bordes, A. (2014). Memory networks. arXiv preprint arXiv:1410.3916.
• Sukhbaatar, S., Weston, J., & Fergus, R. (2015). End-to-end memory networks. Advances in neural information processing systems, 28.
• Kumar, A., Irsoy, O., Ondruska, P., Iyyer, M., Bradbury, J., Gulrajani, I., … & Socher, R. (2016, June). Ask me anything: Dynamic memory networks for natural language processing. In International conference on machine learning (pp. 1378-1387). PMLR.

이 memory의 개념도 RNNsearch(Bahdanau, 2015)를 제안한 동기와 비슷하다. 기존의 recurrence network들이 과거의 정보를 모두 하나의 context vector에 저장하려다 보니 감당이 되지 않을 것이라는 점에서다. 여기에서는 long term memory 장치를 만들었는데 매 단계마다 들어오는 정보를 계속 memory에 저장하여 과거에 대한 정보도 최대한으로 활용하려는 의도가 담겼다.

Memory Networks (MemNN)

그 첫 순서로 memory라는 개념을 network에 들고 온 논문을 살펴보고자 한다. MemNN이라고도 불리는 memory network는 어떤 문장의 나열로 정보가 주어진 다음, 질문이 주어졌을 때 적절한 답을 모델이 출력해야 하는 QA problem을 위한 모델로 제시되었다.

..Overall Structure

MemNN은 크게 네 가지 단계로 움직인다.

1. Input을 feature representation으로 변환한다(embedding).
2. 새로운 input을 메모리에 저장한다(메모리 업데이트).
3. 새로운 input(즉, 질문)에 대하여 관련성 깊은 메모리를 찾는다. 이때 가장 관련성 깊은 메모리, 그다음 관련성 깊은 메모리, …의 방식으로 단계적으로 찾아나간다다.
4. 관련 깊은 메모리를 통하여 output을 도출한다.

구체화를 해보자. 위 방법을 수식으로 구체화해보자.

$I$ component 주어진 input $x$를 전처리하여 $I(x)$로 embedding한다. 어떤 방법을 사용해도 무관하다. 저자는 간단하게 bag or word 기법을 사용했다.

$G$ component 메모리의 빈 공간에 새로이 embedding된 input을 저장한다. 빈 공간에 효율적으로 할당하면 되는데, 빈 공간을 선택하는 함수(상황에 따라 input이 들어올 때마다 1씩 증가하는 함수일 수도 있고, input sequence가 너무 길어지면 hash function을 활용할 수도 있을 것이다) $H(x)$에 대하여 $m_{H(x)} = I(x)$를 수행한다. 저자는 $H$를 간단하게 1씩 늘려갔다(그냥 array 같은 구조를 활용한 듯).

$O$ component 주어진 질문 $x$에 대하여 최적의 답변을 출력하기 위하여 memory에 저장된 관련된 정보를 추출한다. 질문과 메모리에 저장된 정보와의 관련성에 대한 점수를 함수 $s_O$(이 함수에 대한 설명은 아래에서 추가로 한다)를 통해 계산하고, 가장 큰 점수를 얻은 메모리를 반환한다. 즉,

\[o = O(x, \mathbf{m}) = \text{argmax}_{i=1, \cdots, N} s_O(x, \mathbf{m}_i)\]

저자는 질문과 가장 관련 깊은 $k$개의 memory를 추출하고 싶었다. 그러면 위 과정을 $k$번 반복해주면 되는데, 앞서 이미 추출된 memory는 함수 input으로 추가로 넣어 반영해주었다. 즉,

\[\begin{align*} o_1 &= O_1(x, \mathbf{m}) = \text{argmax}_{i = 1, \cdots, N} s_O(x, \mathbf{m}_i), \\ o_2 &= O_2(x, \mathbf{m}) = \text{argmax}_{i = 1, \cdots, N} s_O([x, \mathbf{m}_{o_1}], \mathbf{m}_i), \\ ... \end{align*}\]

를 $k$번 반복하면 된다. 이렇게 다음 component에게 $[x, \mathbf{m}{o_1}, \cdots,\mathbf{m}{o_k}]$를 전달한다.

$R$ component $k$개의 관련된 memory를 활용하여 최종 답안을 도출한다. 여기서는 지금까지 등장한 모든 단어들의 집합 $W$에서 단어를 하나씩 비교하여 가장 관련 깊은 단어 하나를 선택하는 과정을 거친다. 즉,

\[r= \text{argmax}_{w\in W} S_R([x, \mathbf{m}_{o_1}, \cdots,\mathbf{m}_{o_k}], w)\]

이 곧 질문 $x$에 대해 모델이 출력하는 답변이 된다.

..Example

저자는 이에 대해 간략한 예시도 하나 들었다. Memory에 다음과 같은 문장(사실)들이 입력되었다고 가정하자(feature representation을 취하지 않은 상태로 나타냈다).

• Joe went to the kitchen.
• Fred went tot eh kitchen,.
• Joe picked up the milk.
• Joe travelled to the office.
• Joe left the milk.
• Joe went to the bathroom.

이 상태에서 $x =$”Where is the milk now?으로 질문이 주어졌다면 $O$ component는 입력된 정보에서 $x$와 관련 깊은 정보를 선택할 것이다. 여기서 $O$ component가 $k=2$로 작동했다면,

• $\mathbf{m}_{o_1}=$”Joe left the milk.”,
• $\mathbf{m}_{o_2}=$”Joe travelled to the office.”

를 선택하는 식이다. 그리고 $R$ component에서는 이들과 가장 관련이 깊은 단어를 뽑아 $r=$”office”라고 출력하는 것이다.

이질감이 들 법한 부분은 input이 하나의 문장으로 이루어져 있다는 것이다. 일반적으로 번역 모델을 다룰 때는 단어 하나 하나를 input을 가지므로, QA solver로써 작동하는 MemNN을 번역 문제에 적용하기 위해서는 input 형태를 수정할 필요가 있다. 이에 대해서는 곧바로 다룬다.

..Scoring the Relevance

그럼 대체 “관련도”는 어떻게 측정했는지, 즉 함수 $s_O$와 $s_R$는 어떻게 설정된 건지 살펴보자. 이 둘은 똑같은 형태를 띄고 있는데 다음과 같다.

\[s(x, y) = \Phi(x)^T U^T U\Phi(y) = [U\Phi(x)]^T [U\Phi(y)].\]

이때 $\Phi(\cdot)$는 주어진 $x, y$를 embedding하여 feature representation으로 만드는 역할을 하며, $U$는 학습해야 하는 parameter로써 $n\times D$ (이때 $D$는 embedding vector 차원)의 크기를 가진다. 저자는 $k=2$인 경우에 대해 $D=3\vert W\vert$로 세팅했는데, $s_O$와 $s_R$에 주어지는 입력에 따라 각 단어가 $\Phi(\cdot)$에 대한 표현 한 가지, $\Phi(\cdot)$에 대한 표현 두 가지를 모두 독립적으로 학습시키기 위함이라고 한다. 실제로 $D=\vert W\vert$로 실험을 한 결과 성능이 많이 저하되었다고 한다.

..Word Sequnces as Input

앞서 언급하였듯, input이 문장 그 자체가 아니라 단어의 sequence로 받기 위해서는 input을 받는 방식을 조금 수정해야 한다. 저자가 제시한 방법은 바로 segmenter를 활용하는 것이었다. 즉, 단어를 따로 메모리에 저장하지 않고 계속 받으면서 모아두다가 segmenter function에 의해 분리(segment)해야할 때가 오면, 그때까지 모은 단어를 하나의 메모리에 배정하는 것이다. Segmenter는 다음과 같이 정의되는데,

\[\text{seg}(c) = W^T_{seg} [U_S\Phi_{seg}(c)],\]

이때 $W^T_{seg}$는 학습해야할 parameter vector이다. 이렇게 segmentor에 의해 계산되는 값이 threshold $\gamma$보다 크다면 segment해야 하는 순간으로 이해하는 것이다.

..Training Method

이 모델은 주어진 loss function을 최소화하며 최적화시키는 방향으로 SGD를 통해 학습시켰다. Loss function은 $k=2$일 때를 예시를 들면 다음과 같은데, 각 대목마다 margin ranking loss(어떤 기준에 대해 오답과 정답의 차이를 margin unit $\gamma$ 이상만큼 분리되도록 유도하는 loss function)를 활용하였다.

\[\begin{align*}\text{minimize}& \sum_{\bar{f}\ne\mathbf{m}_{o_1} }\max[0, \gamma - s_O(x, \mathbf{m}_{o_1})+ s_O(x, \bar{f})] \\ &+\sum_{\bar{f}'\ne\mathbf{m}_{o_2}} \max[0, \gamma-s_O([x, \mathbf{m}_{o_1}], \mathbf{m}_{o_2}) + s_O([x, \mathbf{m}_{o_1}], \bar{f}')] \\ &+ \sum_{\bar{r}\ne r}\max[0, \gamma-s_R([x, \mathbf{m}_{o_1}, \mathbf{m}_{o_2}], r) + s_R([x, \mathbf{m}_{o_1}, \mathbf{m}_{o_2}], \bar{r})] \end{align*}\]

다만 이 방법의 단점은 network라고 이름붙이긴 했지만 일반적인 신경망 구조를 따르지 않다보니 backpropagation이 안 되어 계산 복잡도가 클 수 있다. 다만 저자 나름대로 최적화를 거쳤는데, loss를 계산할 때마다 모든 summation을 계산한 것이 아닌 loss 계산에 활용할 $\bar{f}, \bar{f}’, \bar{r}$을 sampling하였다고 한다.

End-to-End Memory Networks

다음으로 소개할 모델은 end-to-end MemNN이다. 위에서 소개한 MemNN은 수집한 정보를 저장할 memory 마련하고, 여기에 attention의 아이디어를 결합했다는 것에 의의가 있다. 하지만 다음과 같은 단점이 남아 있었다.

• backpropagation이 불가하여 학습시킬 때 어려움이 있음
• 제시한 각 layer마다($k$개의 관련 memory찾는 component, $R$ component 등) loss 함수를 다 따로 제시하여 최적화시켜야 함

이 모델은 이러한 점을 해결하기 위해 $O$ component를 연속적인 느낌으로 재구성했다(can be considered as a continuous form of the Memory Network). 이 모델은 또 Bahdanau(2015)에서 제시한 RNNsearch하고도 유사한 성격이 있는데, 다만 독립적인 attention을 여러 layer에 걸쳐서 활용했다는 부분이 차별점이 드러난다.

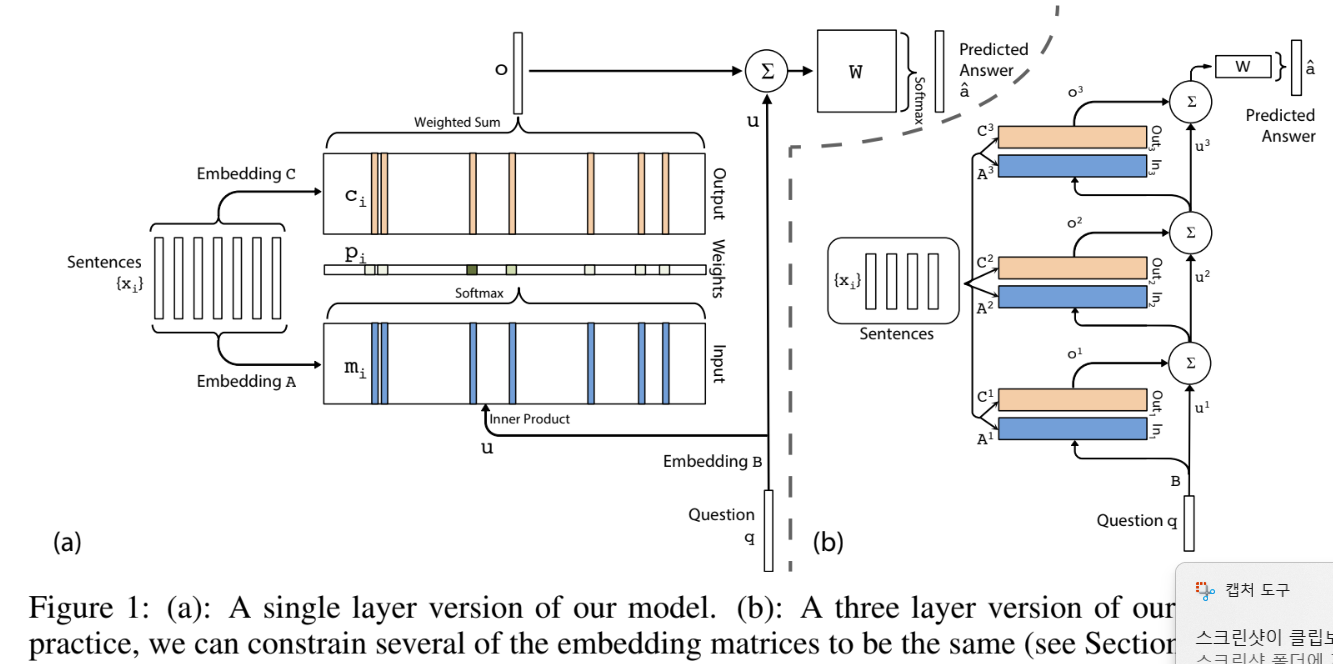
..Overall Structure(Single Layer)

저자는 먼저 attention을 하나만 활용했을 때의 모델을 제시하였다. 이후 attention을 여러 개로 확장하는 작업은 간단하기 때문이다.

Dictionary의 차원을 $V$라고 하자.

Input Memory Representation Input sequence $x_1, \cdots, x_n$는 모두 $d$차원의 벡터에 embedding되어 $m_1, \cdots, m_n$의 형태로 메모리에 저장된다. Query(질문) $q$도 똑같이 embedding되어 $u$의 형태로 저장된다. 두 input 모두 embedding할 때 $d\times V$차원의 parameter를 활용한다.

조금 더 구체적으로 살펴보면, input sequence $x_i$가 단어들의 모음 ${x_{i1}, \cdots, x_{in}}$으로 주어진다면, 각 $x_{ij}$는 bag of words 기법으로 표현된 벡터들이다. 그러면 $d\times V$의 parameter matrix $A$에 의해 메모리에 저장되는 벡터는 \(m_i = \sum_j A\,x_{ij}\)

로 embeddig된다. 하지만 이렇게 embedding하면 단어 순서를 반영하지 못하기 때문에 position encoding도 필요하다. 이를 위해 도구 하나를 도입하는데, 벡터 $l_j$이다. 각 element는 $l_{kj} = (1-j/J)-(k/d)(1-2j/J)$로 이루어져 있는데, 이때 $J$는 문장 내 단어 수이고 $d$는 알다시피 embedding dimension이다. 우리는 embedding 방법을 다음과 같이 수정할 수 있다.

\[m_i = \sum_j l_j^T A\, x_{ij}\]

이어서 input sequence와 query와의 연관성을 inner product로 계산하여 확률의 형태로 나타낸다. 각각은

\[p_i = \text{Softmax}(u^Tm_i)\]

의 확률을 배정받는다.

Output Memory Representation 각각의 input $x_i$는 output으로 출력될 형태를 따로 embedding하여 $c_i$를 만든다. 이때 활용하는 parameter의 size 역시 $d\times V$이다.

그러면 최종 대답을 준비하는 response vector $o$는 출력될 형태의 벡터 $c_i$에, 위에서 계산한 확률을 가중치로 활용하여 계산한다. 즉, attention을 적용한 결과값으로

\[o = \sum_i p_ic_i\]

로 표현할 수 있다. 이 방식은 Bahdanau(2015)의 RNNsearch에서 차용한 attention 기법과 유사하다.

Final Prediction 최종 답안으로 각각의 label이 정답일 확률

\[\hat{a} = \text{Softmax}(W (o+u))\]

을 출력한다. 이때 $W$는 $V\times d$ size의 parameter이다. $o$도 아니고 굳이 $o+u$를 활용한 이유는 아래 multiple layers architecture를 살펴보면서 납득할 수 있을텐데, 귀납적인 편리성을 위한 것으로 추측한다.

..Training

저자는 loss function으로 정답 label $a$와 prediction $\hat{a}$ 간의 cross-entropy을 사용했으며, optimizer로 SGD를 사용했다.

이 모델은 모든 paramter가 continuous한 형태로 하나로 연결되어 있으므로 vanilla MemNN과 다르게 end-to-end로 모델을 학습시킬 수 있다. 따라서 backpropagation을 활용하여 효율적인 모델 학습이 가능하다.

..Structure for Multiple Layers

$(k+1)$번째 layer에서 input으로 활용되는 벡터는 $k$번째 layer의 input에서 output을 더한 값이다. 이는 기존 input에 $k$번째 결과에 따른 영향을 반영한 것으로 해석할 수 있다.

\[u^{k+1} = u^k + o^k\]

가장 위에 있는 layer에서 우리는 다음을 통해 최종 prediction을 도출한다.

\[\hat{a} = \text{Softmax}(W(o^K + u^K))\]

원래 그 다음 layer가 있었다면 input으로 활용되었을 $o^K + u^K$를 최종 prediction을 하는 데에 활용한 것이다.

..Remarks

Multiple-layer version을 가만히 다시 생각해보면 RNN 구조를 위아래로 길게 늘린(그리고 각각의 iteration마다 서로 다른 parameter를 사용하는 느낌) 형태로 생각할 수 있다. 만약 input과 output을 embedding하는 parameter를 매 layer에서 똑같이 활용했다면, 이는 RNN하고 굉장히 비슷해진다. 하지만 RNN과 다른 점이 있다면, 수리적으로 보았을 때 어떤 input을 도출할 때 그 전에 등장한 나오는 모든 output들에 conditioning(조건부 취급)이 된다는 것을 알 수 있다. RNN 이었으면 sequence 하나하나를 입력받을 떄 Markov chain 형태를 띠기 때문에 사실상 직전 입력에 대해서만 conditioning이 된다.

Vanilla MemNN하고도 비교했을 때 MemNN은 관련 깊은 메모리를 직접 추춣하는 형식이었기 때문에 굉장히 discrete하고 hard한 최적화 방식을 취했다. 이 end-to-end MemNN은 전체 memory에 대해서 attention을 취함으로써 조금 더 soft한 최적화를 유도했고, 덕분에 모든 과정이 continuous하게 연결되어 backpropagation도 가능하게 되었다.

마지막으로 주목할 법한 구조적 특징은 모델에서 활용한 input들인데, input에 관한 정보 $m_i$, 질문에 대한 정보 $q$, 그리고 output으로 내보낼 정보 $c_i$, 세 가지 형태의 embedding vector input이 있었다. 이러한 구조를 특별히 강조하지는 않았지만, 이는 transformer모델에서 등장하는 key, query, value와 얼추 대응된다. 그 전에는 attention을 retrieve할 정보를 재조합하기 위해 가중치를 구하는 것으로만 활용했다면, 이 모델에서는 attention에서 활용할 input들을 세 가지 형태의 루트로 정형화한 것이다.

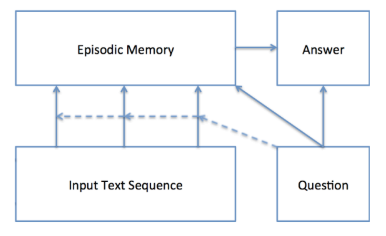
Dynamic Memory Networks(DMN)

Dynamic memory network도 memory network를 확장시킨 유명한 모델이다. End-to-end MemNN와 구조적으로는 차이가 있지만, attention을 여러 번 활용한다는 점에서 공통점을 가진다. 하지만, 앞선 모델과 다르게 attention layer만 반복하는 것이 아니고, attention을 통해 도출된 정보를 분석하여 실질적으로 memory에 내장된 정보를 수정한다. 이렇게 memory를 처음 그대로 두는 것이 아닌, 끊임없이 정보를 반영한다는 의미에서 dynamic memory라는 이름이 붙여졌다. 이를 통해 의미를 하나 찾으면, 그 의미에서 한 단계 나아가서 더 구체적인 의미를 찾고, 이러한 과정을 반복하다 보면 점점 더 구체적인 연관성을 찾을 수 있다.

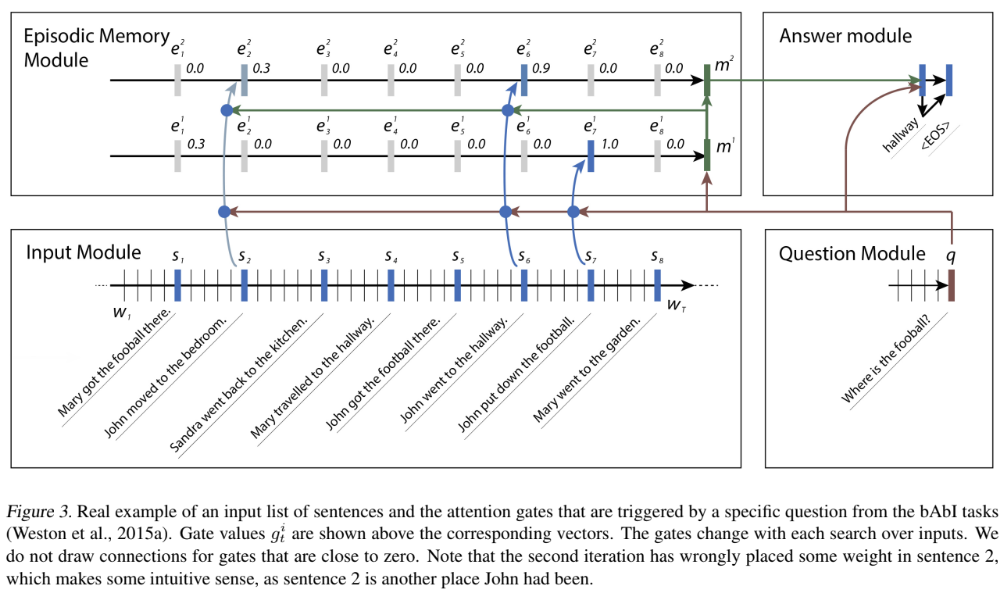
이를테면, Where is the football?이라는 query를 던졌을 때, 첫 번째 iteration에서는 John put down the football.이라는 문장을 선택함으로써 John이라는 정보를 얻었다면, 두 번째 iteration에서는 그렇다면 John의 위치에 대한 정보를 attention을 통해 또다른 가중치를 적용함으로써 정보를 업데이트하게 된다.

..Overall Structure

Input Module QA problem에서는 여러 문장을 입력받아야 한다. 저자는 문장들을 하나의 문장으로 모두 이었고, 그래도 문장을 구분하기 위해 각 문장이 끝나는 부분에 token을 하나씩 삽입하였다. 그렇게 하여 결국 하나의 문장을 입력하는 형태가 된 것이다.

Encoder로써 활약을 크게 한 recurrent network를 활용하여 문장을 통째로 embedding하였다. 그중에서도 저자가 선택한 모듈은 GRU이다. 그렇게 하여 각 단어마다 출력되는 hidden state $h_t$가 바로 주변 정보를 반영한 embedding된 벡터 역할을 한다.

\[h_t = \text{GRU}(Lw_t, h_{t-1})\]

이때 $L$은 단어 하나하나를 embedding하는 parameter matrix이다.

비슷한 과정으로 query로 주어지는 문장도 GRU를 활용하여 embedding한다.

\[q_t = \text{GRU}(Lw^Q_t, q_{t-1})\]

하지만 모든 hidden state를 활용하는 것은 아니고, 가장 마지막 hidden state $q = q_{T_Q}$만을 활용한다.

기본적인 embedding을 마쳤다면, DMN에서 작동하는 모델의 구조는 다음과 같다.

Episodic Memory Module 여러 차례 attention 등의 모듈을 활용하여 과정을 반복하면서 memory를 업데이트한다. 이 모듈을 episodic memory module이라고 부른다. 현재 메모리 상태가 $m^{i-1}$이고, attention등을 활용하여 추가로 만들어진 정보(episode)를 $e^i$라고 하면, memory는

\[m^i = \text{GRU}(e^i, m^{i-1})\]

로 업데이트된다. 이때 초기 memory로 $m^0 = q$를 활용한다.

이제 각 단계에서 episode가 만들어지는 과정을 살펴보자. Attention을 중심으로 정보가 만들어지는데, attention에 들어가는 정보는 여기서도 총 세 가지이다.

• $c_t$: a candidate fact (-> key)
• $m^{i-1}$: a previous memory $m^{i-1}$ (-> value)
• $q$: a query (-> query)

Attention score는 함수 $G$에 의해 계산되는데, 이 $G$는 단순히 $(c_t, m^{i-1}, q)$를 입력으로 받는 것이 아닌 더 고차원의 벡터 $z(c, m, q)$를 입력받는다. 이 $z$는 성분 간의 유사도를 다양한 방법으로 평가하기를 시도하며, 다음과 같다.

\[\begin{align*} z&(c, m, q) = \\ &[c, m, q, c^Tq, c^Tm, \vert c-q\vert, \vert c-m\vert, c^TW^{(b)}q, c^TW^{(b)}m] \end{align*}\]

이렇게 하여 계산되는 attention score는

\[\begin{align*} g^i_t &= G(c_t, m^{i-1}, q) \\ &=\sigma[W^{(2)}\tanh (W^{(1)}z(c, m, q) + b^{(1)}) + b^{(2)}] \end{align*}\]

이다. 이 가중치는 정답 후보 $c_i$를 input으로 가지는 GRU에 활용되는데, GRU에 어느 정도까지 의존할지를 결정한다. 그리고 마지막 hidden state를 최종 episode 값으로 사용한다.

\[\begin{align*} h_t^i &= g_t^i \text{GRU}(c_t, h_{t-1}^i) + (1-g_t^i)h_{t-1}^i, \\ e^i &= h_{T_C}^i. \end{align*}\]

Answer Module 이렇게 반복하여 최종 memory값 $a_o = m^{T_M}$을 얻는다. 마지막으로 연속되는 GRU에 query 값을 계속 같이 넣으면서 최종 정답을 도출한다.

\[\begin{align*} y_t &= \text{Softmax}(W^{(a)}a_T), \\ a_t &= \text{GRU}([y_{t-1}, q], a_{t-1}). \end{align*}\]

학습은 cross-entropy loss를 최소화하는 방향으로, SGD를 optimizer로 진행하였다고 한다.

..Remarks

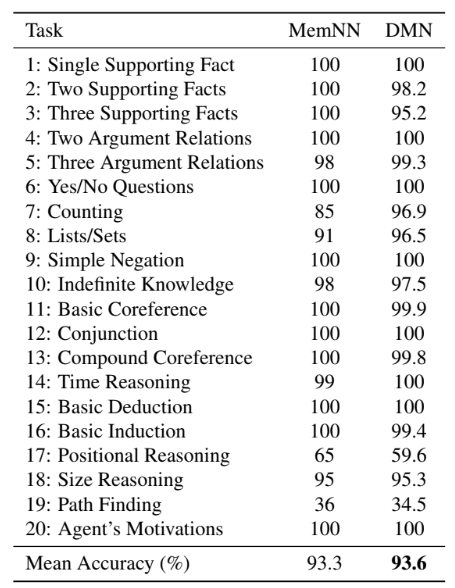
비록 GRU를 너무 과하게 사용하여 parameter 수가 많아진 감이 있다. 하지만 많은 QA problem field에서 vanilla MemNN보다 우위를 점하고 있다.

여기서 주목해야 할 점은 attention을 역시 세 가지 루트로 나누어 사용했다는 것과, attention을 반복 사용함으로써 memory 정보를 업데이트했다는 것이다. 이렇게 반복 작업을 하는 것이 단순히 parameter 수가 많아져서 정보를 잘 파악했다고 보기보다는, 문장의 의미를 저장하는 기준이 여러 가지이기이고 이러한 반복되는 구조가 그러한 특징을 잘 담아낸다고 보는 것이 옳을 것이다. 그리고 그 의도대로 모델이 학습되고 있음을 다음 자료를 통해 간접적으로 엿볼 수 있다.

Conclusion

세 논문을 통해 attention의 구조를 정형화했고, 반복해서 사용한다는 것의 의미를 사례를 들어 설명했다. 이렇듯 Transformer 등장 전에 여러 연구에서 attention을 효과적으로 사용할 방법에 대해서 많은 고민을 거쳤다.

다음 리뷰에서는 inter-과 intra-attention을 소개하기에 적절한 논문을 리뷰하고자 한다. 이 두 구조는 Transformer에서도 적극적으로 활용된 바 있다. 그러므로 이 둘의 차이점은 무엇이고, 어떤 구조에 반영하려는 시도가 있었는지를 함께 살펴보면서 Transformer 구조에 한 걸음 더 다가가기로 한다.

Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio. (2015). Neural machine translation by jointly learning to align and translate. In Proceedings of ICLR.

Ashish Vaswani and Noam Shazeer and Niki Parmar and Jakob Uszkoreit and Llion Jones and Aidan N. Gomez and Lukasz Kaiser and Illia Polosukhin. (2017). Attention Is All You Need. In Advances in Neu-ral Information Processing Systems 30: Annual Conference on Neu-ral Information Processing Systems 2017.