Cramer-Rao Bound and Fisher Information(크래머-라오 유계와 피셔 정보)
Hammersley-Chapman-Robbins inequality
지금까지는 unbiased estimator 중에서 최소의 variance를 갖는 estimator인 UMVUE에 대해서 알아보았다. 여기서는 어떤 주어진 prameter $theta$에 대하여 unbiased estimator가 어느 정도까지 분산을 최소화할 수 있는지 그 lower bound를 보여주는 유명한 inequality를 유도할 것이다. 그리고 그 어느 unbiased estimator가 이 variance에 도달하게 되면, 그 estimator는 가장 효율적인 performance를 가진다고 말할 수 있다.
Unbiased estimator의 lower bound를 엉성하게 만들어보기 위해 어떤 model $\mathcal{P}=\{P_{\theta}: \theta\in\Omega\}$의 unknown parameter $\theta\in\Omega$와 $g(\theta)$를 estimate하는 unbiased estimator $\delta$, 그리고 어떤 random variable $\psi$에 대하여 다음을 생각해보자.
\[Var_{\theta}(\delta)\ge\frac{Cov_{\theta}^2(\delta, \psi)}{Var_{\theta}(\psi)}\]Lower bound를 만들기 위해서는 먼저 우변은 $\delta$와 관련되지 않는 편이 좋을 듯하다. 그러므로 이렇게 만들기 위해 $\psi$를 정말 잘 선택해주어 분자의 covariance term항을 $\delta$와 무관하게 만들어주면 완벽할 것 같다. 다음 과정을 따라가보자.
$\theta +\Delta\in\Omega$인 $\Delta$에 대하여, $\delta$는 unbiased하므로
\[E_{\theta+\Delta}\delta - E_{\theta}\delta = g(\theta+\Delta)-g(\theta)\]이다. 우변은 $\delta$와 무관한 식임을 주목하라. 이제 $E_{\theta+\Delta}\delta - E_{\theta}\delta$를 $P_{\theta}$아래에서의 어떤 covariance로 표현해보자. 그러면 그렇게 줄인 covariance는 결국 $\delta$와 무관한 식으로 완성될 것이다.
먼저는 $P_{\theta+\Delta}$ 아래의 expectation $E_{\theta+\Delta}\delta$를 $P_{\theta}$ 아래의 expectation으로 표현하면 좋아보인다. 이를 위해 우리는 likelihood ratio가능도비를 정의할 것이다. 이전 post에서 data의 joint density $p_{\theta}(x)$는 likelihood를 나타냄을 언급한 적이 있다(Mathematical Statistics - Minimal sufficiency and completeness 편 참조). 이 joint density를 data $x$에 대한 함수로 바라보지 말고 $\theta$에 대한 함수로 한 번 바라본다면, 만약 true value의 $\theta$가 대입된다면 그 true value는 data를 가장 잘 설명하는 $\theta$의 값이 될 것이므로 likelihood의 값이 가장 커질 것이다. 이는 결국 다르게 말하면 true value $\theta_0$에 대하여 data $X$가 $P_{\theta_0}$에서 추출되었을 가능성이 가장 높다는 것을 시사하는 것이다. 그러한 면에서 likelihood는 true value estimate를 파악할 때 중요한 도구로 활용된다. Likelihood ratio는 두 개의 다른 $\theta$에 대하여 likelihood의 ratio를 나타낸 것이다. 이 likelihood ratio는 hypothesis testing가설 검정을 할 때 다시 등장하여 중점적으로 다루게 될 것이다.
여기서도 ratio를 다음과 같이 정의하자.
\[L(x) = \frac{p_{\theta+\Delta}(x)}{p_{\theta}(x)},\quad p_{\theta}(x) >0\]$p_{\theta}(x)=0$인 구간에서는 $L(x) = 1$로 정의할 것이다. 여기서는 $p_{\theta}(x)=0$이면 $p_{\theta+\Delta}(x)=0$이라는 아주 주요한 가정이 내포되어 있다. 이제 expectation $E_{\theta+\Delta}\delta$를 의도한 바와 같이 표현이 가능하다.
\[E_{\theta+\Delta}h(X) = \int hp_{\theta+\Delta} \,d\mu = \int hLp_{\theta}\,d\mu = E_{\theta}L(X)h(X)\]위에서 $h = 1$을 대입하면 $E_{\theta}L = 1$, $h = \delta$를 대입하면 $E_{\theta+\Delta}\delta = E_{\theta}L\delta$임을 이용하여, 적절히 잡아야했던 $\psi$를
\[\psi(X) = L(X) - 1\]로 놓는다면 $E_{\theta}\psi = 0$이므로
\[E_{\theta+\Delta}\delta - E_{\theta}\delta = E_{\theta}L\delta - E_{\theta}\delta = E_{\theta}(L-1)\delta = E_{\theta}\psi\delta = Cov_{\theta}(\delta, \psi)\]이다. 따라서 우리는 $Cov_{\theta}(\delta, \psi) = g(\theta+\Delta) - g(\theta)$를 얻음으로써 $\delta$와 무관한 식을 얻었다. 이를 이용하여 $\delta$의 variance의 lower bound를 만들어보면
\[Var_{\theta}(\delta) = \frac{Cov_{\theta}(\delta, \psi)}{Var_{\theta}(\psi)} = \frac{[g(\theta+\Delta) - g(\theta)]^2}{Var_{\theta}(L(X)-1)} = \frac{[g(\theta+\Delta)-g(\theta)]^2}{E_{\theta}\left(\frac{p_{\theta+\Delta}(X)}{p_{\theta}(X)}-1\right)^2}\]가 된다. 이 bound를 우리는 Hammersley-Chapman-Robbins inequality(bound) 혹은 줄여서 Chapman-Robbins inequality(bound)라고 부른다.
Fisher Information
위의 inequality에서 우리는 조금 더 나아가보자. Differentiability와 integral과 differentiation 순서 교환에 관한 regulation conditions 아래에서 dominated convergence에 의해 $\Delta\to0$을 취하면 우리는
\[\begin{align*} \frac{[g(\theta+\Delta)-g(\theta)]^2}{E_{\theta}\left(\frac{p_{\theta+\Delta}(X)}{p_{\theta}(X)}-1\right)^2} &= \frac{\left[\frac{g(\theta+\Delta)-g(\theta)}{\Delta}\right]^2}{E_{\theta}\left(\frac{[p_{\theta+\Delta}(X) - p_{\theta}(X)]/\Delta}{p_{\theta}(X)}\right)^2} \\ &\to \frac{[g'(\theta)]^2}{E_{\theta}\left(\frac{1}{p_{\theta}(X)}\frac{\partial p_{\theta}(X)}{\partial\theta}\right)^2} \end{align*}\]임을 얻을 수 있는데, 이때 마지막 term의 분모의 값은 눈여겨 볼 필요가 있다. 분모를 다시 표현하면
\[I(\theta):= E_{\theta}\left(\frac{\partial\log p_{\theta}(X)}{\partial\theta}\right)^2\]으로 나타내어지는데, 이를 Fisher information피셔 정보, 혹은 줄여서 그냥 information정보라고 한다. 잠시 Fisher information에 관하여 더 설명하고자 한다.
Fisher information은 다음 방법으로도 다시 표현할 수 있다. 이는 증명이 간단하게 가능하므로 독자에게 남길까 한다.
\[\begin{align*} I(\theta) &= E_{\theta}\left(\frac{\partial\log p_{\theta}(X)}{\partial\theta}\right)^2 \\ &= Var_{\theta}\left(\frac{\partial\log p_{\theta}(X)}{\partial\theta}\right) \\ &= -E_{\theta}\frac{\partial^2\log p_{\theta}(X)}{\partial\theta^2} \end{align*}\]세 번째 표현식은 가장 계산이 편리하기 때문에 많이 활용한다. 왜 위의 표현식이 information의 양을 나타내는지 알아보기 위해 Fisher information을 조금 더 통계적으로 해석해보자. 기본적으로는 model에 의해 estimate되고자 하는 unknown parameter $\theta$를 data $X$가 어느 정도까지 반영되고 있는지, 그 정보의 양을 수치화한 것이라고 볼 수 있다. 먼저 $\log p_{\theta}(x)$, 즉 likelihood에다가 logarithm을 씌운 값을 log-likelihood로그 가능도라고 부른다. 예를 들어 i.i.d. random sample data의 log-likelihood는 independence에 의해 각 data의 density를 logarithm한 것의 합이라고 볼 수 있다. 여기서 우리가 관심있게 살펴볼 것은 log-likelihood의 derivative
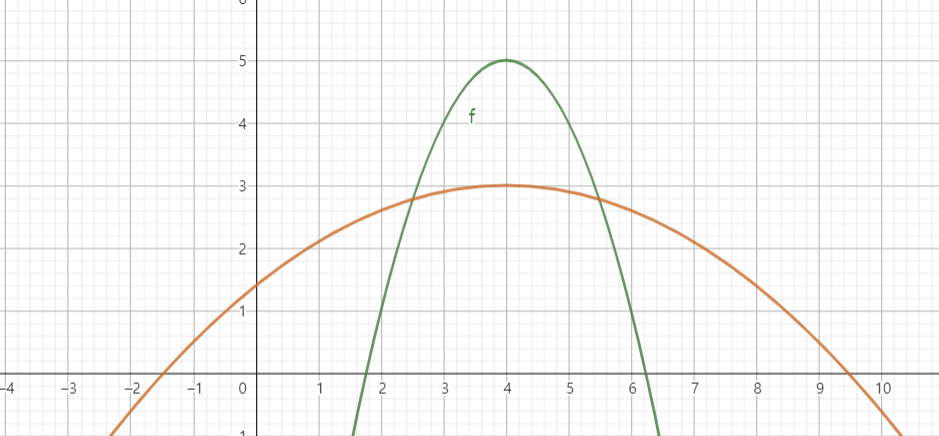
\[\frac{\partial}{\partial\theta}\log p_{\theta}(x)\]이다. 이를 우리는 score점수라고 부른다. 앞에서도 언급했지만 만약 어떤 $\theta$에 대하여 likelihood가 maximize된다면, 그 $\theta$는 data의 분포를 가장 잘 설명해준다고 해석할 수 있으므로 그 $\theta$가 실제 true value에 가깝다고 볼 수 있다. 하지만 log-likelihood 역시 data가 어떻게 주어지냐에 따라 그 값이 달라지기 마련이다. 때문에 log-likelihood의 형태에 따라 data를 다시 얻었을 때 log-likelihood가 maximize되는 지점이 거의 바뀌지 않아 estimate가 정확할 수도 있지만, 한편으로는 maximize되는 지점이 너무 많이 바뀌어 true value에 대한 estimate가 어려울 수도 있다. 이는 다음 그림을 통해 더 쉽게 이해가 가능하다.
만약 log-likelihood가 초록색 그래프의 개형을 띈다면 위의 논리에 의해 estimate하기 더 쉬워질 것이다. 그만큼 $X$가 $\theta$에 대한 정보를 많이 가지고 있기 때문에, true value에서 조금이라도 벗어난다면 log-likelihood의 값이 더 급격하게 변화함을 알 수 있다. 궁극적으로 $\theta$에 따른 기울기의 변화가 더 심하다면 data는 $\theta$에 대한 정보를 더 많이 담고 있다고 해석할 수 있고, 이를 보여주는 것이 score의 variance이다. 혹은 second derivative를 관찰한다고도 볼 수 있다. 이 모든 것을 나타내는 수치가 Fisher information이었던 것이다.
Example 11.1 Model $\mathcal{P} = \{P_{\theta}:\theta\in\Omega\}$가 dominated family이고 density $p_{\theta}$와 Fisher information $I$를 가지고 있다고 하자. 우리는 model parameter의 reparameterization을 통해 Fisher information이 어떻게 변화하는지 관찰하고자 한다. $\Xi$에서 $\Omega$로 가는 one-to-one function $h$에 대하여 family $\mathcal{P}$를 $\tilde{\mathcal{P}} = \{Q_{\xi}: \xi\in\Xi\}$로 reparameterize했다고 하자. 그러면 $Q_{\xi}$는 $q_{\xi} = p_{h(\xi)}$의 density를 가질 것이다. 어떤 $\theta$에 대하여 $\theta = h(\xi)$인 $\xi$가 존재하고, $\tilde{P}$의 Fisher information $\tilde{I}$는 다음과 같이 도출된다.
\[\begin{align*} \tilde{I}(\xi) &= \tilde{E}_{\xi}\left(\frac{\partial\log q_{\xi}(X)}{\partial\xi}\right)^2 = \tilde{E}_{\xi}\left(\frac{\partial \log p_{h(\xi)}(X)}{\partial\xi}\right)^2 \\ &= [h'(\xi)]^2 E_{\theta}\left(\frac{\partial \log p_{\theta}(X)}{\partial\theta}\right)^2 = [h'(\xi)]^2 I(\theta) \end{align*}\]
Cramer-Rao Bound
다시 돌아와서 우리는 Chapman-Robbins inequality에서 한 단계 더 나아가 Fisher information을 이용한 bound를 잡을 수 있는데 이것이 Cramer-Rao bound이다.
Theorem 11.2 (Cramer-Rao) Open set $\Omega$에 대하여 model $\mathcal{P} = \{P_{\theta}: \theta\in\Omega\}$가 dominated family임에 따라 density $p_{\theta}$를 가지고, $\theta$에 대하여 differentiable할 때, 모든 $\theta\in\Omega$에 대하여 finite한 variance를 가지는 모든 $g(\theta)$의 unbiased estimator $\delta$에 대하여 다음이 성립한다.
\[Var_{\theta}(\delta)\ge \frac{[g'(\theta)]^2}{I(\theta)}, \quad \forall\theta\in\Omega\]
만약 $g(\theta)=\theta$라면, Cramer-Rao bound는 다음과 같이 간소화된다.
\[Var_{\theta}(\delta)\ge \frac{1}{I(\theta)}, \quad \forall\theta\in\Omega\]즉, $\theta$의 unbiased estimator $\delta$의 precision한국어로모름(variance의 reciprocal역수를 일컫는 말로, Bayes에서 많이 쓰는 표현이다)의 upper bound가 Fisher information까지라는 것을 의미하기도 한다.
사실 위의 식은 $\psi = \partial\log p_{\theta}/\partial\theta$ 으로 놓으면 금방 유도가 가능하다. 이렇게 $psi$를 놓는 것과 likelihood ratio를 이용하여 $\psi$를 놓는 것이 정말 비슷한 맥락임을 알 수 있는 것은
\[\frac{\partial}{\partial\theta}\log p_{\theta} = \frac{1}{p_{\theta}}\frac{\partial p_{\theta}}{\partial\theta}\]으로 본다는 점에서 $p_{\theta}$를 기준으로 likelihood가 $\theta$에 따라 얼만큼 변화하는지를 보여주는 것으로 해석 가능한데, lkelihood ratio에서 1을 뺀 것도 마찬가지 논리임을 알 수 있다.
물론 Cramer-Rao bound가 unbiased estimator의 variance의 최솟값을 의미하진 않는다. 다시 말하여, 이는 결국 lower bound를 제시해줄 뿐 실제로 어떤 상황에서는 이 bound variance를 가지는 unbiased estimator를 가지지 않는 경우도 있다. 그럼에도 어떤 unbiased estimator는 bound의 값을 가지는 variance를 소유하고 있을 때도 있는데, 이때의 unbiased estimator를 fully efficient하다고 표현하기도 한다. 그렇지만 Cramer-Rao bound를 이끌어내기 위해서 우리는 꽤나 많은 regularity를 가정하였음을 잊어서도 안 된다. 이 condition이 성립하지 않는 경우에 대해서는 Cramer-Rao bound보다 더 작은 variance를 가지는 estimator $\delta$가 충분히 있을 수 있기 때문이다.
Example 11.3 Model이 exponential family에 속할 때를 살펴보자. $\mathcal{P}$를 one-parameter canonical exponential family라고 하면, density $p_{\eta}$는 다음과 같은 꼴로 나타낼 수 있다.
\[p_{\eta}(x) = \exp[\eta T(x) - A(\eta)]h(x)\]Data가 오직 하나의 point밖에 없다고 하자. 그러면 $p_{\eta}$는 likelihood로도 역할을 한다. 이때 log-likelihood의 derivative인 score는
\[\frac{\partial \log}{\partial\eta} = T - A'(\eta)\]이므로 $\mathcal{P}$의 Fisher information은
\[I(\eta) = Var_{\eta}(T - A'(\eta)) = Var_{\eta}(T) = A''(\eta)\]혹은 log-likelihood의 second order derivative가 $-A’’(\eta)$라는 점에서도 바로 유도가 가능하다.
만약 이 exponental family를 $\mu = A’(\eta) = E_{\eta}T$로 parameterize하면 Example 11.1에 의하여
\[I(\eta) = A''(\eta) = [A''(\eta)]^2\cdot I(\mu)\]가 되고, $A’’(\eta) = Var(T)$라는 점에서
\[I(\mu) = \frac{1}{Var_{\mu}(T)}\]임이 보여진다. $T$가 $\mu$의 UMVUE임에 입각하면, Cramer-Rao bound $Var_{\mu}(\delta)\ge 1/I(\mu)$의 variance를 가지는 estimator가 존재하는 경우이며, lower bound가 곧 minimum이 된 case이다.
만약 independent한 두 single point data $X, Y$가 수집되었다면, 전체 Fisher information은 각각의 data의 Fisher informatino으로 쪼개질 수 있다. $X$는 density $p_{\theta}$, $Y$는 density $q_{\theta}$를 가진다고 가정하면(각각의 model이 서로 다른 measure에 의해 dominate되었을 수도 있다) 두 data의 joint density는 $p_{\theta}q_{\theta}$이다. 따라서 전체 Fisher information은
\[\begin{align*} I_{X, Y}(\theta) &= Var_{\theta}\left(\frac{\partial\log[p_{\theta}(X)q_{\theta}(Y)]}{\partial\theta}\right) \\ &=Var_{\theta}\left(\frac{\partial\log p_{\theta}(X)}{\partial\theta}+\frac{\partial\log_{\theta}(Y)}{\partial\theta}\right) \\ &=Var_{\theta}\left(\frac{\partial\log p_{\theta}(X)}{\partial\theta}\right)+Var_{\theta}\left(\frac{\partial \log q_{\theta}(Y)}{\partial\theta}\right) \\ &= I_X(\theta) + I_Y(\theta) \end{align*}\]으로 쪼개짐을 알 수 있다. 위의 사실은, 만약 우리가 $n$개의 independent한 data point를 얻었을 때 전체 Fisher information은 $nI(\theta)$가 됨을 알 수 있다. 이때 $I(\theta)$는 data point가 하나일 때의 Fisher information이다.
Variance Bounds in Higher Dimensions
지금까지는 $\theta$가 $\mathbb{R}$, 1차원에 놓였을 때의 variance bound를 알아보았다. 하지만 위의 결과들은 $\theta\in\mathbb{R}^s$일 때, 즉 $s$차원일 때까지 확장할 수 있다. 이때의 Fisher information은 더이상 어떠한 값이 아닌 matrix 꼴을 가질 것이다.
\[\begin{align*} I(\theta)_{i, j} &= E_{\theta}\left[\frac{\partial\log p_{\theta}(X)}{\partial\theta_i}\frac{\partial\log p_{\theta}(X)}{\partial\theta_j}\right] \\ &= Cov_{\theta} \left(\frac{\partial\log p_{\theta}(X)}{\partial\theta_i}, \frac{\partial\log p_{\theta}(X)}{\partial\theta_j}\right) \\ &= -E_{\theta}\left[\frac{\partial^2\log p_{\theta}(X)}{\partial\theta_i\partial\theta_j}\right] \end{align*}\]이렇게 element-wise하게 표현할 수도 있겠지만, 고~급지게 matrix 표현을 빌린다면
\[\begin{align*} I(\theta) &= E_{\theta}(\nabla_{\theta}\log_{\theta}(X))(\nabla_{\theta}\log_{\theta}(X))^T \\ &= Cov_{\theta}(\nabla_{\theta}\log p_{\theta}(X)) \\ &= -E_{\theta}\nabla_{\theta}^2 \log p_{\theta}(X) \end{align*}\]또, 1차원일 때 log-likelihood의 derivative의 expectation이 0이었던 것처럼, 여기서도 log-likelihood의 gradient의 expectation은 0의 값을 가진다.
\[E_{\theta}\nabla_{\theta}\log p_{\theta}(X) = 0\]이 성질을 이용하면 위의 세 개의 equality를 쉽게 증명할 수 있다.
$g(\theta)$의 unbiased estimator $\delta$에 대하여 Cramer-Rao bound는 자연스레 다음과 같이 표현됨을 알 수 있다.
\[Var_{\theta}(\delta) \ge[\nabla g(\theta)]^T I^{-1}(\theta) [\nabla g(\theta)]\]그리고 dominated family $\mathcal{P} = \{P_{\theta}: \theta\in\Omega\}$의 density $p_{\theta}$와 Fisher information $I$에 대하여, 역시 $\Xi$에서 $\Omega$로의 one-to-one function $h$를 이용하여 reparameterization하면 우리는 family $\tilde{\mathcal{P}} = \{Q_{\xi}:\xi\in\Xi\}$를 얻는다. 이때 $Q_{\xi} = P_{h(\xi)}$이다. 그러면 density 또한 $q_{\xi} = p_{h(\xi)}$의 관계가 성립할 것이고, 어떤 $\theta$와 $\theta = h(\xi)$를 만족하는 적절한 $\xi$에 대하여, chain rule에 의해
\[\frac{\partial \log q_{\xi}(X)}{\partial\xi_i} = \sum_j \frac{\partial\log p_{\theta}(X)}{\partial\theta_j}\frac{\partial h_j(\xi)}{\partial\xi_i}\]가 성립한다. $h$의 partial derivative는 matrix 형태로 다음과 같이 표현된다면
\[[Dh(\xi)]_{i, j} = \frac{\partial h_i(\xi)}{\partial\xi_j}\]우리는 $\tilde{\mathcal{P}}$의 Fisher information이 다음과 같이 표현됨을 알 수 있다.
\[\begin{align*} \tilde{I}(\xi) &= \tilde E_{\xi}[\nabla_{\xi}\log q_{\xi}(X)][\nabla_{\xi}\log q_{\xi}(X)]^T \\ &= E_{\theta} [Dh(\xi)]^T [\nabla_{\theta}\log p_{\theta}(X)][\nabla_{\theta}\log p_{\theta}(X)]^T[Dh(\xi)] \\ &= [Dh(\xi)]^T I(\theta)[Dh(\xi)] \end{align*}\]마지막으로 exponential family에 적용하면 어떻게 되는지 알아보자. 만약 $\mathcal{P}$가 $s$-parameter canonical exponential family 라고 하고 density는 다음의 꼴을 가진다고 하면,
\[p_{\eta}(x) = \exp [\eta\cdot T(x) - A(\eta)]h(x)\]log-likelihood의 second order derivative는
\[I(\eta)_{i, j} = -\frac{\partial^2 A(\eta)}{\partial\eta_i \partial\eta_j}\]이므로 Fisher information은 다음과 같아진다.
\[I(\eta)_{i, j} = \frac{\partial^2 A(\eta)}{\partial\eta_i \partial\eta_j}\]조금 더 멋있게 matrix form으로 적어보면
\[I(\eta) = \nabla^2 A(\eta)\]이다.
다음 편에서는 조금 특별한 exponential family를 살펴볼 예정이다. Curved exponential family라고 불리우는 것인데, $T_i$끼리 어떠한 관계를 만족하는 등의 이유로 full rank가 되지 않는 것들이다. Full rank의 경우 원래 $T$가 complete sufficient해서 minimal sufficient였는데, 이들은 항상 minimal이라고 하여 complete하지 않을 수도 있는 등의 다른 점이 있다. 이들의 성질을 다음 글에서 더 알아보기로 한다.