Curved Exponential Families(곡선지수족)

이번 편에서는 curved exponential family의 성질에 대해서 다루어보고자 한다. Full rank exponential family와는 다르게 curved exponential family는 $\eta_i$ 간의 constrain이 존재하거나 $\eta(\Omega)$의 interior가 없이 어떤 관계를 지니는 등 조금 특별한 경우의 exponential family를 의미한다. 때문에 full rank의 $T$가 complete, minimal sufficient한 성질을 지닌 만능의 statistic이었다면, curved exponential family에서의 $T$는 minimal sufficient 할지는 몰라도 complete가 되지 않는 등 여러 다른 점이 존재한다. 이러한 성질을 차례로 파악해보고, 이러한 형태의 exponential family를 model로 자주 활용하는 sequential experiment에 대해 이어서 살펴볼 것이다.

Constrained Families

$\mathcal{P}= \{P_{\eta}:\eta\in\Xi\}$는 full rank $s$-parameter canonical exponential family라고 하자. 그러면 이 family에서의 $T$는 complete sufficient할 것이다. 우리는 이때 submodel, 즉 $\mathcal{P}$의 일부 $\mathcal{P}_0$를 살펴보고자 한다. Submodel $\mathcal{P}_0$를 $\theta\in\Omega\subset\mathbb{R}^r$에 대하여 $\tilde{\eta}(\theta)$로 parameterize했다고 하자. 즉,

\[\mathcal{P}_0 = \{P_{\tilde{\eta}(\theta)}: \theta\in\Omega\}\]

인 셈이다.

거의 대부분의 경우 parameterize를 한다고 하면 $\tilde{\eta}:\Omega\to\Xi$를 bijective(=one-to-one and onto)로 잡곤 한다. 그러면 $\theta$의 관한 식으로 표현하나 $\eta$에 관한 식으로 표현하나 차이가 없고 다루기 더 편리한 쪽을 택하면 된다. 당연하게도 $\mathcal{P} =\mathcal{P}_0$이다. 이땐 $\mathcal{P}_0$가 curved는 아니다.

$\mathcal{P}_0$를 통해 curved exponential family를 얻기 위해서는 기본적으로 $\mathcal{P}_0$가 $\mathcal{P}$와 같은 것이 아닌, 진짜 strict submodel이어야 하고, $\Omega$의 차원 $r$이 원래 parameter space $\Xi$의 차원 $s$보다 작아야 하지 않겠는가? 이렇게 차원이 줄어드는 경우에는 다음의 두 가지 유형이 있다.

1. $\tilde(\Omega) = \{\tilde{\eta}(\Omega): \theta\in\Omega\}$ 위의 점 $\eta$가 nontrivial linear constraint를 만족하는 경우다. 이 경우, 몇 개의 $\eta_i$가 다른 $\eta_j$’s 들에 linear combination으로 표현된다는 이야기므로 실질적인 paramter 차원은 줄어들게 된다. 즉, $\mathcal{P}_0$는 $q\lt s$에 대하여 $q$-parameter exponential family가 된다. 여기에서의 $T$는 sufficient는 충분히 되나 $\eta(\Omega)$의 interior가 없기 때문에 $\tilde{\eta}(\Omega)\ominus\tilde{\eta}(\Omega)$가 $\mathbb{R}^s$ 전체를 span하지 못하므로 minimal sufficient까지 되진 못한다(이에 관한 더 자세한 내용은 Mathematical Statistics - Minimal Sufficiency and Completeness편의 Example 8.4를 참조하라). 당연히 complete도 불가능하다.
2. $\tilde{\eta}(\Omega)$가 linear constraint를 만족하지 않는 경우다. 이 때는 $\tilde{\eta}(\Omega)$의 interior는 존재한다는 점에서 $T$가 minimal sufficient하지만, full rank는 여전히 아니라는 점에서 $T$가 complete까지는 아닐 수 있다.

이렇게 이론적으로만 보면 너무 헷갈리니 예시를 한 번 살펴보자.

Example 12.1 Data가 만약 $N(\mu, \sigma^2)$으로부터 추출되었다고 하면, 이들의 joint density는 2-parameter canonical exponential family를 형성하며, 이때의 canonical parameter는

\[\eta = \left(\frac{\mu}{\sigma^2}, -\frac{1}{2\sigma^2}\right)\]

이고,

\[T = \left(\sum_i X_i, \sum_i X_i^2\right)\]

인 complete sufficient statistic이다. 여기서 우리는 submodel을 하나 잡을 것인데 mean과 variance가 동일한 normal distribution의 family로 설정할 것이다. 그러면 $\mu$와 $\sigma^2$을 하나의 parameter인 $\theta$로 parameterize할 수 있고 subfamily는 모두 $N(\theta, \theta),\,\theta>0$의 형태일 것이다. 그러면 canonical parameter는 다시 다음과 같이 parameterized된 parameter로 바뀐다.

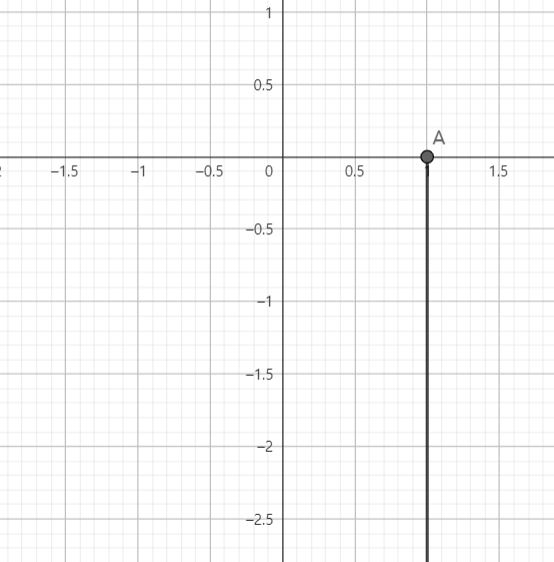
\[\tilde{\eta}(\theta) = \left(1, -\frac{1}{2\theta}\right)\]

여기서 $\tilde{\eta}(\theta)$의 꼴을 보면, $\tilde{\eta}{\Omega}$는 linear constraint $\eta_1 = 1$을 만족함을 알 수 있다. 아래 그림에서도 표현되었 듯이, $\tilde{\eta}(\Omega)$의 interior가 없다(아래 그림에서 $(1, 0)$은 불포함이어야 한다).

물론 interior가 없다고 하여 무조건 $T$가 minimal하지 않은 것은 아니지만, 여기서는 오로지 linear한 constraint가 있기 때문에 $\tilde{\eta}(\Omega)$가 span하지 못하는 성분이 있을 수밖에 없다. 그러한 면에서 $T$는 minimal하지 않다. 실제로 joint density를 구해보면, 이 submodel는 full rank one-parameter exponential family이고, 2차원의 exponential family는 아님을 알 수 있다. $\sum_i X_i^2$을 canonical form의 complete sufficient statistic을 가지지만, $T$가 comple sufficient한 것은 아니다.

이번에는 mean의 절댓값과 standard deviation이 같은 submodel만을 고려해보자. 즉, $\sigma=\vert\mu\vert$이므로 submodel은 $N(\theta, \theta^2),\,\theta\in\mathbb{R}$을 고려하고 있다. 이때의 parameterized parameter는

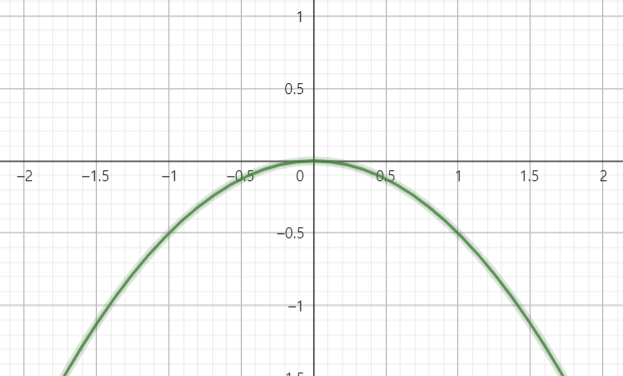
\[\tilde{\eta}(\theta) = \left(\frac{1}{\theta}, -\frac{1}{2\theta}\right)\]

이다. 이 경우 $\tilde{\eta}(\Omega)$는 parabola_포물선 형태를 띤다는 것을 알 수 있다(역시 $(0, 0)$은 불포함이어야 한다).

이 경우 이 submodel은 curved exponential family를 형성함을 알 수 있고, $T$는 minimal sufficient하다(언급했지만 $\tilde{\Omega}$의 interior가 있으면 무조건 $T$는 minimal이지만, interior가 없다고 하여 $T$가 꼭 minimal하지 않은 것은 아니다). 하지만 $T$는 complete하지 않다. 그 이유를 살펴보기 위해 먼저 모든 $\theta$에 대하여 expectation이 0이 나오는 statistic을 하나 찾아보자(completeness의 정의를 활용하기 위함이다). $T = (T_1\, T_2)^T$에 대하여

\[\begin{align*} E_{\theta}T_1^2 &= (E_{\theta}T_1)^2 + Var_{\theta}(T_1) = n^2\theta^2 + n\theta^2 \\ E_{\theta} T_2 &= n((E_{\theta}X_i)^2 + Var_{\theta}(X_i)) = 2n\theta^2 \\ \end{align*}\]

이다. 위의 결과들을 이용하면 우리가 원하는 statistic 하나를 찾을 수 있다.

\[E_{\theta} (2T_1^2 - (n+1)T_2) = 0, \quad \theta\in\mathbb{R}\]

만약 $T$가 complete했다면 $g(T) = 2T_1^2 - (n+1)T_2$도 항상 0이 도출되어야 할 텐데 $n=1$이 아닌이상 그렇지 않다. 따라서 $T$는 complete하지 않다.

기초통계에서 우리가 two sample에 대해서 비교할 때 equivariance_등분산을 가정하고 inference를 많이 거쳤었다. 그때 등장했던 것이 바로 pooled sample variance인데, 공통된 varinace를 estimate할 statistic으로 활용했었다. 이를 curved exponential family의 관점에서 다시 한 번 살펴보도록 하자.

Example 12.2 우리는 두 개의 independent한 population $N(\mu_x, \sigma_x^2)$과 $N(\mu_y, \sigma_y^2)$으로부터 각각 $X = (X_1, \cdots, X_m)$와 $Y = (Y_1, \cdots, Y_n)$의 data를 얻었다고 하자. 그러면 이들의 joint distribution은 4-parameter exponential family를 형성하게 되며, 대응되는 parameter는 $\theta = (\mu_x, \mu_y, \sigma_x^2, \sigma_y^2)$이다.

\[T = \left(\sum_{i=1}^m X_i, \sum_{j=1}^n Y_j, \sum_{i=1}^m X_i^2, \sum_{j=1}^n Y_j^2\right)\]

은 여기서 sufficient statistic이며,

\[\eta = \left(\frac{\mu_x}{\sigma_x^2}, \frac{\mu_y}{\sigma_y^2}, -\frac{1}{2\sigma_x^2}, -\frac{1}{2\sigma_y^2}\right)\]

는 여기서 canonical parameter이다. $T$와 equivalent한 간소화된 sufficient statistic은

\[T = (\overline{X}, \overline{Y}, S_x^2, S_y^2)\]

으로 볼 수 있다. 이때 $S_x^2$와 $S_y^2$은 각각 $X$와 $Y$의 sample variance로 다음과 같이 놓았다.

\[S_x^2 = \frac{\sum_{i=1}^m (X_i-\overline{X})^2}{m-1}, \quad S_y^2 = \frac{\sum_{i=1}^n (Y_i-\overline{Y})^2}{n-1}\]

만약 두 data로부터 variance가 공통이라고 합의했을 때, 즉 $\sigma_x^2 =\sigma_y^2=\sigma^2$일 때, $\eta$에 대해선 $\eta_3 - \eta_4=0$라는 linear constraint가 성립하게 된다. 이로써 만들어지는 submodel은 curved는 아님을 알 수 있다. Submodel에서 $T=(\overline{X}, \overline{Y}, S_x^2, S_y^2)$는 complete sufficient하지 않으며 minimal도 아니다. 하지만 Submodel 자체만으로 다시 분석했을 때 차원은 4에서 3으로 줄어들었지만 3-parameter exponential family임을 알 수 있고, 여기서의 sufficient statistic으로 도출되는 $(T_1, T_2, T_3+T_4)$은 complete하다. 이것과 equivalent한 complete sufficient statistic은 $(\overline{X}, \overline{Y}, S_p^2)$인데, 이때의 $S_p^2$을 pooled sample variance라고 부르며 다음과 같이 정의한다.

\[S_p^2 = \frac{\sum_{i=1}^m (X_i-\overline{X})^2 + \sum_{i=1}^n (Y_i-\overline{Y})^2}{n+m-2} = \frac{(m-1)S_x^2 + (n-1)S_y^2}{n+m-2}\]

$S_x^2$과 $S_y^2$는 independent하기 때문에 $(n+m-2)S_p^2/\sigma^2 \sim \chi_{n+m-2}^2$를 통해 inference를 이어갈 수 있었다.

만약 두 data로부터 mean이 공통이라고 합의했을 때, 즉 $\mu_x = \mu_y$일 때 만들어지는 submodel은 $\eta_1/\eta_2 = \eta_3/\eta_4$의 constraint를 가지므로 curved exponential family이다. 이때 $T=(\overline{X}, \overline{Y}, S_x^2, S_y^2)$는 minimal sufficient이긴 하지만 complete하진 않음을 알 수 있다. 이는 $E_{\theta}(\overline{X}-\overline{Y})=0,\,\forall\theta\in\Omega$이 $\overline{X}-\overline{Y}\equiv 0$을 의미하지 않기 때문이다.

Sequential Experiments

어떤 experiment가 sequential하다는 것은 experiment의 performance가 이전에 관측했던 data의 information에 영향을 받아 design되는 것을 일컫는다. 이를 테면, experiment를 특정 시점에서 종료해버릴지 계속 진행할지 결정하는 것은 sequential experiment라고 볼 수 있다. 이는 사전에 관측된 data의 information에 기반하여 결정하게 될 것이지, 그 시점에서 independent하게 결정할 일은 아니다. 혹은, sampling을 할 수 있는 population 선택지가 여러 개일 때, 그중 population에서 할 지 결정하는 것도 과거의 data에 기반한 과정이 될 수 있다.

Sequential experiment가 일반적인 experiment보다 주목받는 이유가 몇 가지 있다. 첫 번째로는 sequential experiment가 효율적인 면이 있다는 것이다. 얼마나 효율적인지는 나중에 decision theory에서 더 다루게 될 것이지만 experiment를 할 때 투자되는 cost까지 고려한 risk를 줄일 수 있다는 장점이 있다. 두 번째로는 상황상 sequential experiment밖에 적용되지 않는 경우가 있기 때문이다. 그중 하나인 다음 예시를 살펴보자.

Example 12.3 우리는 population size를 estimate하고자 한다. $M$마리의 물고기가 있는 연못을 하나 생각하자. $M$은 unknown parameter이고, 우리는 $M$을 estimate할 수 있는 experiment를 구성하는 것이 목표이다. 이를 위해 data는 capture-recapture 방식을 통해 수집될 것이다. 이 experiment는 다음 두 가지 과정을 수반한다.

1. $k$마리의 물고기를 sample하여 표식한다. 그리고 다시 연못으로 돌려보낸다. 표식들은 모두 동일하여 구분이 되진 않는다.
2. 물고기가 다시 연못으로부터 sample된다. 이때 표식된 물고기를 건질 probability는 $\theta = k/M$이다(물론 이는 표식된 물고기와 표식되지 않은 물고기가 잡힐 가능성이 동등할 때의 이야기이고, 실제로는 조금 과한 전제일 수 있다). $\theta$로 다시 표현하면

\[M = \frac{k}{\theta}\]

이므로, 결국 우리는 $1/\theta$를 estimate하는 것이 좋아보인다. 두 번째 step에서 수집한 data는 Bernoulli distribution으로 modeling이 가능할 것이다. Sample $X_1, \cdots, X_N$이 $\text{Ber}(\theta)$로부터 추출되었다고 하자. $N$은 sample size이고, $X_i$는 표식된 물고기면 1, 아니면 0을 나타낸다. Sample size를 $N=n$으로 잠시 고정해두자. 그러면 우리는 다음의 joint density를 얻는다.

\[p_{\theta}(x) = \prod_{i=1}^n \theta^{x_i}(1-\theta)^{1-x_i} = \theta^{\sum x_i}(1-\theta)^{n-\sum x_i}\]

이때 $T(x) = \sum x_i$는 sufficient statistic이며 위의 density의 형태는 exponential family에 속함을 보여준다. $E_{\theta} = n\theta$임에 따라 $T/n$는 UMVUE임을 알 수 있다. 하지만 불행하게도 $1/\theta$를 estimate하기 위한 UMVUE는커녕, unbiased estimator 자체가 없을 가능성도 있다.

\[E_{\theta}\delta(T)\le \max_{0\le k\le n} \delta(k)\]

에서, $\theta$가 너무 과하게 작으면 $1/\theta$는 값이 갑자기 엄청 커질 것이고 위의 우변보다 훨씬 웃도는 값일 수도 있다는 것이다. $\theta$가 우리가 고정한 sample size $n$에 대하여 $1/n$보다 작다면 $T=0$일 probability가 1에 가까울 것이다 .장 문제인 것은 $T = 0$이면 우리는 $\theta$에 대한 아무런 information도 얻을 수 없다는 점이다. 간단한 예로, 표식을 한 물고기가 100마리 당 한 마리 꼴이고 우리가 sampling한 물고기가 고작 10마리뿐이라면, 표식이 된 물고기를 전혀 얻지 못할 수 있다. 이때 $1/\theta = 100$으로 꽤 큰 숫자이지만, 표식이 된 물고기를 아에 못 얻는 경우 우리는 $\theta$에 대한 정보를 전혀 얻을 수 없고, 한 마리를 얻는 경우에서 각각 estimate를 해도 $\theta$의 reciprocal을 25정도로 예측할 것이다. 결국 100이라는 숫자를 estimate하고 싶어도 sample size가 작게 설정되면(모종의 이유로) underestimate되는 등 specify하기 너무 어렵다. 그리고 고작 표식된 물고기 한 마리 더 얻는다는 이유로 estimate 값이 너무 심하게 vary하여 더욱이 true value를 specify하지 못한다는 문제가 있다. 이럴수가!

Inverse binomial sampling 방법은 이러한 문제를 해결해준다. 위에서는 sample size $N$을 어떤 특정 값으로 고정해두었지만, 이번에는 딱히 고정해두진 않을 것이다. 대신에 $m$개의 $X_i$들이 1이 되는 즉시 experiment를 그만할 것이다. 그러면 $N$은 random variable이 되고 이 experimental design은 사전의 관측된 data에 의해 결정되므로 sequential함을 알 수 있다. 이러한 방법으로 추출된 data는 다음의 형태일 것이다.

\[X = (X_1, \cdots, X_N)\]

물론 조금의 technical한 문제가 있다면 $N$이 random variable이기 때문에 $X$가 몇 차원 vector인지 알 수 없어서 random vector라고 부르기엔 좀 그렇다는 점이다. 이 경우 data를 바라보는 가장 자연스러운 방법은 experiment 자체에 involve되는 성질들을 모두 event로 취급하여 $\sigma$-field를 구성하는 것이다. 이를 테면, $\{T = k\}$나 $\{N = 7\}$같은 사전 관측치의 summary나 experiment의 횟수 등을 의미하는 것들을 event로 모두 포함시킬 수 있다. 이는 나중에 stochastic process와 함께 다루어질 것이다. 여기에서는 $Y_i$를 $(i-1)$번째 표식된 물고기까지 모았을 때 $i$번째 표식된 물고긱까지 모으는 데 sampling한 물고기 수라고 하면 event를 $Y = (Y_1, \cdots, Y_m)$라는 random vector로 복잡하기 않게 표기할 수 있다.

아무쪼록, 이렇게 experiment를 design하면 위의 문제가 어떻게 해결되는지 관찰해보자. 위에서 정의한 $Y_i$는 서로 independent하고 identical한 distribution에서 추출되었음을 알 수 있고, 그 distribution은 다음과 같이 도출할 수 있다.

\[\begin{align*} P_{\theta}(Y_i = y) &= P(X_1 = 0, \cdots, X_y = 0, X_{y+1}=1) \\ &= (1-\theta)^y\theta \\ &= \exp(y\log{(1-\theta)} + \log{\theta}), \quad y = 0, 1, \cdots \end{align*}\]

위의 mass function을 가지는 distribution은 geometric distribution_기하분포임이 알려져 있다. 이는 one-parameter exponential family이고 canonical parameter $\eta = \log(1-\theta)$와 $A(\eta) = -\log\theta = -\log(1-e^{\eta})$을 가지고 있다. Exponential family의 property에 의해

\[E_{\theta}Y_i = A'(\eta) = \frac{e^{\eta}}{1-e^{\eta}} = \frac{1-\theta}{\theta}\]

$Y_1, \cdots, Y_m$의 joint density는

\[p_{\theta}(y) = \exp\left[\sum_i y_i\cdot \log(1-\theta) + \log\theta\right]\]

로써 complete sufficient statistc $T = \sum_{i=1}^m Y_n = N-m$(전체 sampling한 횟수 $N$에서 $m$마리의 표식된 물고기를 뽑는 것은 $Y_i$에 count되지 않는다)을 가지고 있다. 이러한 $T$가 따르는 distribution은 negative binomial distributuion임을 알고 있다. 여기서 $T$의 mass function은 다음과 같을 것이다.

\[P(T = t) = {m+t-1\choose m-1}\theta^m(1-\theta)^t, \quad t = 0, 1\]

여기에서

\[E_{\theta}T = mE_{\theta}Y_i = \frac{m}{\theta} - m\]

이므로 $1/\theta$의 UMVUE는

\[\frac{T+m}{m} = \frac{N}{m}\]

임을 알 수 있다.

위의 예시를 통해 어떤 상황에서 sequential experiment가 떄론 필요하게 되는지 알고, 활용을 어떻게 하면 되는지도 잘 알아보았다. 조금 더 formal하게 어떻게 하면 이 experiment 상에서 density를 표현할 수 있을지 생각해볼 것이다. 먼저 sequential experiment는 experiment를 $N$에서 멈출 때까지 data $X_1, X_2, \cdots$를 계속 수집한다. 이때 experiment를 멈추는 횟수 $N$은 data에 따라 dependent하게 정해져도 되지만, 언제 멈출 지 예상한다는 등의 것들은 불가능하다고 가정하자. 이 멈추는 횟수 $N$의 성질을 잘 나타내게끔 표현하는 방법은, set of sequence $A_1, A_2, \cdots $에 대하여

\[{N = n} = {(X_1, \cdots, X_n)\in A_n}, \quad n= 1, 2, \cdots\]

라고 하면 된다. 이제 density를 어떻게 표현하면 되는지 다음 theorem을 보면서 살펴보자.

Theorem 12.4 Data $X_1, X_2, \cdots$가 i.i.d.이고 각각이 common density $f_{\theta}, \theta\in\Omega$에서 추출되었다고 하자. 만약 모든 $\theta\in\Omega$에 대하여 $P_{\theta}(N<\infty) = 1$(즉, 실험이 언젠가 종료되긴 한다)이면, 전체 data $(N, X_1, \cdots, X_n)$ (물론 이런 식의 표현은 precise하지 않으며, 나중에 observe data는 $\sigma$-field로 취급할 것이다) 는 다음과 같은 joint density를 가진다.

\[\prod_{i=1}^n f_{\theta}(x_i)\]

만약 $f_{\theta}$가 다음의 꼴을 가지는 exponential family의 일종이라고 하면

\[f_{\theta}(x) = \exp[\eta(\theta)\cdot T(x) - B(\theta)]h(x)\]

이들의 joint density(혹은 likelihood)는

\[\exp\left[\eta(\theta)\cdot\sum_{i=1}^n T(x_i) - nB(\theta)\right]\prod_{i=1}^n h(x_i)\]

역시 exponential family이며, canonical parameter $\eta_1(\theta), \cdots, \eta_s(\theta), -B(\theta)$와 sufficient statistic $(\sum_{i=1}^N T(X_i), N)$를 가진다.

위의 theorem만 보면, $N$이 random variable을 취급받는 바람에 canonical parameter에 $-B(\theta)$라는 element가 하나 더 추가된 것 말고는 원래 experiment와 똑같다. 하지만, 여기에서 도출된 estimator의 distribution을 조사해보면 멈추는 시각 $N$에 상당한 영향을 받는 편이다. 이를 테면, 원래 $\overline{X} = (X_1+\cdots+X_n)/n$은 $E_{\theta}X_1$의 unbiased estimator였지만, 여기에서의 $(X_1+\cdots +X_N)/N$은 $E_{\theta}X_1$의 biased estimator이다. 또, canonical parameter에 추가로 붙은 $-B(\theta)$ element가 이야기해주는 것은 sequential experiment는 modeling 시 주로 curved exponential family를 활용하게 됨을 알 수 있다. Example 12.3에서 $X_1+\cdots +X_m = m$으로 $N$과 무관하게 항상 일정하다는 면에서 inverse binomial model은 일반적인 sequential experiment에서 나타나는 density의 형태와는 조금 다르고 특별한 case라고 볼 수 있다.

다음 예시는 실제로 sequential experiment에서는 $\overline{X}$이 distribution의 mean을 estimate하기 위한 unbiased estimator로 활용할 수 없음을 보여준다.

Example 12.5 $X_1, X_2$가 각각 failure rate $\lambda$인 exponential distribution을 independent하게 따르는 sequential experiment를 생각하자. $X_1$부터 관측을 시작하는데, $X_1\lt 1$이면 더이상의 관측을 하지 않지만 만약에 $X\ge 1$이면 $X_2$까지 관측한다. 그러므로 $X_1<1$이면 $N = 1$이고, $X_1\ge 1$이면 $N=2$인 셈이다.

먼저 이 data의 joint sample을 살펴보자. $N$이 사실상 random variable인 상황이므로 Theorem 12.4에서 설정했던 바와 같이 $(N, X_1, \cdots, X_n)$를 data로 보고 joint density를 찾는다.

\[p_{\theta}(x) = \lambda^n e^{-\lambda\sum_{i=1}^n x_i} = \exp\left[\lambda\sum_{i=1}^n + \log\lambda \cdot n\right]\]

Exponential family에 속하는 것을 알 수 있고, canonical parameter

\[\eta = (-\lambda, \log\lambda)\]

와 sufficient statistic

\[T = (\sum_{i=1}^N X_i, N)\]

를 가지는 curved two-parameter exponential family임을 알 수 있다. 우리는 합리적으로 $\overline{X}$를 exponential family의 mean인 $1/\lambda$를 estimate하는데 활용할 수 있을 것이라고 고려할 수 있다. 만약 $\overline{X}$가 unbiased estimator라면, 이는 $T_1/T_2$로 $T$에 대한 함수이다. 그러므로 곧 UMVUE가 될 것이다. 하지만, 실제로 $\overline{X}$의 expectation을 구해보면 unbiased하지 않음을 알 수 있다.

\[\overline{X} = \begin{cases} X_1 & X_1\lt 1 \\ \displaystyle \frac{X_1+X_2}{2} & X_1 \ge 1 \\ \end{cases} = X_1 + \begin{cases} 0 & X_1 \lt 1 \\ \frac{X_2 - X_1}{2} & X_2\ge 1 \\ \end{cases}\]

로 표현되고, exponential distribution의 memorylessness_무기억성과 $X_1, X_2$의 independence에 의하여

\[\begin{align*} E_{\lambda}[X_1\vert X_1 >1] &= E_{\lambda}[X_1+1] = \frac{1}{\lamdba}+1 \\ E_{\lambda}[X_2\vert X_1 >1] &= E_{\lambda}[X_2] = \frac{1}{\lamdba} \\ \end{align*}\]

이 성립하고, 따라서 $\overline{X}$의 expectation은

\[E_{lambda}\overline{X} = E_{\lambda}X_1 + E_{\lambda}\left[\frac{X_2-X_1}{2}\vert X_1\ge 1\right]P(X_1\ge 1) = \frac{1}{\lambda}-\frac{e^{-lambda}}{2}\]

가 된다. 즉 true value보다 평균적으로 underestimate하고 있음을 알 수 있다.

— 다음 글에서는 conditional distribution을 measure theory에 입각하여 엄밀하게 정의한다. 수리적으로 상당히 많이 techinical한 편이다. Conditional distribution의 수학적 정립이 끝나면, 이전에 소개하지 못했던 factorization theorem의 증명을 conditional distribution의 수학적 표현에 기반하여 해보고자 한다.