Several Types of Convergence(확률수렴, 분포수렴)

이번 편에서는 다시 원래의 맥락으로 돌아가 large sample theory를 다룰 것이다. 이 내용 역시 frequentist의 심장같은 철학을 수학적으로 나타내는 도구라고 볼 수 있다. 이들이 probability를 정의할 때 infinte sequence of experiment에서 어떤 특정 event의 frequency로 정의했으므로 experiment를 무한 번 진행했을 때 어떻게 되는지, 다시 말하여 sample의 개수가 infinte할 때 어떻게 되는지가 매우 중요한 것이다. 그리고 이들의 논리가 맞춰지기 위해서는 sample size를 무한이 늘렸을 때 어떤 estimate 값이 true value로 다가가야 한다. 이와 관련된 성질이 consistency_일치성이며, 위와 같은 이유로 frequentist는 estimator가 consistency를 만족하는지의 여부를 굉장히 중요시한다. 그러므로 large sample theory는 estimator가 과연 frequentist의 핵심 가치인 consistency를 만족하는지, 혹은 infinie size일 때 estimator가 따르는 distribution이 무엇일지 파악하여 근사하는 방법론을 제시해주는 것이 목적이 되겠다. 또한, estimator 각각을 sample size를 infinte하게 키웠을 때 여전히 존재하는 variance 등을 비교하면서 performance를 다시금 비교해볼 것이다. Large sample theory는 몇 편에 나누어서 연재되는데, 다양한 convergence와 limit theorem 등을 다루고, 실제 estimator들의 performance를 비교하는 metric을 다룰 예정이다.

Convergence in Probability

Random variable이 converge한다는 것은 그 값이 어느 정도 범위 내에 모이는 probability가 굉장히 높아졌을 때를 의미한다.

Definition 19.1 Sequence of random variables $Y_n$이 $n\to\infty$에 따라 random variable $Y$로 converge in probability한다는 것은, 모든 $\epsilon\gt0$에 대하여 $n\to\infty$이면

\[P(\vert Y_n - Y\vert \ge\epsilon)\to 0\]

이라는 것이다. 이때 표기는

\[Y_n\overset{p}{\to} Y\]

라고 한다.

가장 기본적인 property부터 알아보자.

Theorem 19.2 (Chebyshev’s Inequality) 임의의 random variable $X$와 임의의 constant $a>0$에 대하여

\[P(\vert X\vert \ge a) \le \frac{EX^2}{a^2}\]

이 성립한다.

Proof: 임의의 $X$에 대하여 다음이 성립함을 알 수 있다.

\[I\{\vert X\vert \ge a\} \le \frac{X^2}{a^2}\]

이제 위에 expectation만 씌우면 결론이 도출된다.

Proposition 19.3 $n\to\infty$임에 따라 $E(Y_n - Y)^2\to0$이면, $Y_n\overset{p}{\to}Y$이다.

Proof: Chebyshev’s inequality(Theorem 19.2)에 의하여 임의의 $\epsilon>0$에 대해

\[P(\vert Y_n - Y\vert \ge\epsilon) \le \frac{E(Y_n - Y)^2}{\epsilon^2}\to 0\]

이므로 증명되었다.

이를 활용하여 sample mean이 꽤나 주요한 property를 가지고 있음을 알 수 있다.

Example 19.4 $X_1, \cdots, X_n$이 mean은 $\mu$이고 variance는 $\sigma^2$인 population으로부터 i.i.d. 하게 추출된 sample이라고 하고, 이때의 sample mean을 $\overline{X}_n = (X_1+\cdots+X_n)/n$이라고 하자. 그러면

\[E(\overline{X}_n - \mu)^2 = Var(\overline{X}_n) = \sigma^2/n \to 0\]

이므로 $n\to\infty$임에 따라 $\overline{X}_n\overset{p}{\to}\mu$를 만족한다.

이는 심지어 $\sigma = \infty$여도 $E\vert X_i\vert\lt\infty$이면 성립함이 알려져 있다. 이 주요한 성질을 weak law of large numbers_{약한 큰 수의 법칙}이라고 한다.

다음 성질은 매우 요긴하게 활용할 것이다.

Proposition 19.5 만약 $f$가 $c$에서 continuous하고 $Y_n\overset{p}{\to}c$라고 할 때, $f(Y_n)\overset{p}{\to}f(c)$라고 한다.

Proof: $f$가 $c$에서 continuous하기 때문에, 임의의 $\epsilon>0$에 대하여 다음을 만족하는 $\delta_{\epsilon}$이 존재한다.

\[\vert y - c\vert\lt\delta_\epsilon\Rightarrow\vert f(y) - f(c)\vert\lt\epsilon\]

그러므로

\[\begin{align*} \{e: \vert Y_n(e) - c\vert\lt \delta_{\epsilon} \}&\subset \{e: \vert f(Y_n(e)) - f(c)\vert \lt \epsilon\} \\ P(\vert Y_n - c\vert\lt\delta_{\epsilon})&\le P(\vert f(Y_n) - f(c)\vert \lt\epsilon) \\ P(\vert f(Y_n) - f(c)\vert \ge\epsilon)&\le P(\vert Y_n-c\vert \ge\delta_{\epsilon})\to 0 \end{align*}\]

으로 $f(Y_n)\overset{p}{\to}f(Y)$임을 증명하였다.

Convergence in probability도 어떤 probability measure 아래에서 따지냐에 따라 달라질 수 있다. 그러므로 어떤 probability distribution의 family $\mathcal{P} = \{P_{\theta}: \theta\in\Omega\}$가 parameter $\theta$를 가지고 있을 때, distribution $P_{\theta}$ 아래에서의 convergence in probability를 표현할 때에는 $\overset{P_{\theta}}{\to}$의 기호를 사용할 것이다.

이제 frequentist가 estimator의 자질로써 가장 중요하게 생각하는 또다는 property 하나를 다룰 것인데, 바로 consistency_일치성이다.

Definition 19.6 $g(\theta)$의 sequence of estimators $\delta_n$($n\ge1$)가 $g(\theta)$에 대하여 consistent하다는 것은, 모든 $\theta\in\Omega$에 대하여

\[\delta_n \overset{P_{\theta}}{\to} g(\theta)\quad \text{as}\quad n\to\infty\]

가 성립함을 의미한다.

Sample mean도 $\mu$에 대한 unbiased estimator라고 볼 수 있는데, 이 역시 consistency를 만족함을 Example 19.5에서 알 수 있다. 그러므로 sample mean은 $\mu$에 대한 꽤나 performance가 좋은 estimator라고 볼 수 있다. 이러한 의미에서 Weak law of large numbers는 i.i.d. sample에서의 sample mean $\overline{X}_n$이 $\mu$에 대한 estimator로써 consistency를 가짐을 보여주는 아주 중요한 법칙이라고 볼 수 있다.

사실 weak law of large numbers는 i.i.d. sample에서만 성립하는 것은 아니다. 조금 확장해서 sample끼리의 어느 정도 약한 correlation이 있을 때에도 충분히 성립할 수 있다. 다음 예시를 살펴보자.

Example 19.7 Random sample $X_1, X_2, \cdots$가 $m$-dependent라고 불리는 것은, $\vert i-j\vert\ge m$에 대하여 $X_i$와 $X_j$가 independent할 때이다. 어떤 random sample $X_1, X_2, \cdots$가 $m$-dependent하다고 하고, $EX_1 = EX_2 = \cdots = \xi$이고 $Var(X_1) = Var(X_2) = \cdots=\sigma^2\lt\infty$이다. Sample mean $\overline{X}_n = (X_1+\cdots+ X_n)/n$에 대하여 $n\to\infty$임에 따라 $\overline{X}_n\overset{p}{\to}\xi$임을 보일 것이다.

Chebyshev’s inequality에 의하여

\[P(\vert \overline{X}_n - \xi\vert \gt\epsilon) \lt \frac{E(\overline{X}_n - \xi)^2}{\epsilon^2} = \frac{Var(\overline{X}_n)}{\epsilon^2}\]

이므로 우리는 적절히 $Var(\overline{X}_n)$를 bound시키면 된다. 한편, $\vert i-j\vert \lt m$에 대하여 $X_i$와 $X_j$는 dependent하고, 둘의 covariance는 bound되어 있다.

\[Cov(X_i, X_j) \le Var(X_i)Var(X_j) = \sigma^2\]

고정된 $i$에 대하여 $Cov(X_i, X_j)>0$인 $j$는 많아봐야 $(2m-1)$개이므로

\[Var(\overline{X}_n) = \frac{1}{n^2}\sum_i\sum_j Cov(X_i, X_j) \le \frac{1}{n^2}\sum_i (2m-1)\sigma^2 = \frac{2m-1}{n}\sigma^2\]

이다. 따라서 $n\to\infty$임에 따라 $Var(\overline{X}_n)/\epsilon^2\to 0$이고, $\overline{X}_n$은 $\xi$에 대하여 consistent함을 증명하였다.

Consistent한 estimator의 예시를 하나 더 살펴보자.

Example 19.8 $X_1, X_2, \cdots$가 failure rate가 $\lambda$인 exponential family에서 i.i.d.로 추출되었다고 하자. $X_{(n)} = \max{X_1, \cdots, X_n}$이라고 할 때, $\log(n)/X_{(n)}$이 $\lambda$에 대한 consistent한 estimator임을 증명할 것이다.

먼저 $X_{(n)}$의 CDF는

\[\begin{align*} F_{X_{(n)}}(t) = P(X_{(n)}\le t) &= P(X_i\le t,\, \forall i) \\ &= (1 - e^{-\lambda t})^n \end{align*}\]

이다. 이를 이용하면

\[\begin{align*} P\left(\bigg\vert \frac{\log{n}}{X_{(n)}} - \lambda\bigg\vert \gt\epsilon\right) &= P\left(\lambda-\epsilon\gt\frac{\log{n}}{X_{(n)}}\quad\text{or}\quad\frac{\log{n}}{X_{(n)}}\gt\lambda+\epsilon\right) \\ &= P\left(\frac{\log{n}}{X_{(n)}}\gt\lambda+\epsilon\right)+1-P\left(\frac{\log{n}}{X_{(n)}}\gt\lambda-\epsilon\right) \\ &= \left(1 - e^{-\lambda\cdot\frac{\log{n}}{\lambda+\epsilon}}\right)^n +1 - \left(1 - e^{-\lambda\cdot{\frac{\log{n}}{\lambda-\epsilon}}}\right)^n\\ &= \left(1 - n^{-\frac{\lambda}{\lambda+\epsilon}}\right)^n+1-\left(1-n^{-\frac{\lambda}{\lambda-\epsilon}}\right)^n \\ &\to 0 + 1 -1 =0 \quad \text{as}\quad n\to\infty \end{align*}\]

따라서 $\log{n}/X_{(n)}$은 consistent하다.

Squared error loss 아래에서 risk $R(\theta, \delta_n) = E_{\theta}(\delta_n - g(\theta))^2$을 보통 $\delta_n$에 따른 mean squared error라고 자주 표현한다. 그러면 우리는 consistency와 risk와의 관계를 찾을 수 있는데, 만약 $n\to\infty$임에 따라

\[R(\theta, \delta_n)\to 0, \quad\forall \theta\in\Omega\]

를 만족하면 Proposition 19.3에 따라 $\delta_n$은 consistent하게 된다. 또, bias와 variance와의 관계도 찾아보면 bias의 제곱과 variance를 더한 것이 risk가 되므로, $n\to\infty$임에 따라 모든 $\theta\in\Omega$에 대하여 bias $b_n(\theta)\to0$이고 variance $Var_{\theta}(\delta_n)\to 0$이면 $\delta_n$이 consistent하다. 그만큼 consistency를 만족시키기 위한 충분조건이 상당히 강함을 알 수 있다.

Convergence in probability의 개념은 어렵지 않게 더 높은 차원으로 확장시킬 수 있다. $Y, Y_1, Y_2, \cdots$를 $\mathbb{R}^p$에 속한 random vector라고 할 때, $Y_n$이 $Y$로 convergent in probability하다는 것은, 모든 $\epsilon >0$에 대하여

\[P(\Vert Y_n - Y\Vert \gt \epsilon) \to 0 \quad \text{as}\quad n\to \infty\]

표기할 때는 동일하게 $Y_n\overset{p}{\to} Y$로 한다. 정의로부터 우리는 각 element가 convergent in probability하면, 즉 각 $i = 1, 2, \cdots, p$에 대하여 $n\to\infty$임에 따라 $[Y_n]_i\overset{p}{\to} [Y]_i $이면, $Y_n\overset{p}{\to} Y$이다. 이는 norm의 성질을 이용하면 쉽게 증명이 가능하다.

이 역시 $c$에서 continuous한 함수 $f:\mathbb{R}^p\to\mathbb{R}^q$에 대하여 $Y_n\overset{p}{\to} Y$이면 $f(Y_n)\overset{p}{\to}f(c)$가 성립한다. 그러므로 $f(x, y) = x+y$ 혹은 $f(x, y) = xy$를 적용하면, 만약 $n\to\infty$임에 따라 $X_n\overset{p}{\to}a$이고 $Y_n\overset{p}{\to}b$가 성립하면, $n\to\infty$임에 따라

\[\begin{align*} X_n + Y_n &\overset{p}{\to} a + b \\ X_nY_n &\overset{p}{\to} ab \end{align*}\]

가 성립한다.

Convergence in Distribution

이제 분포 자체가 수렴하는 것에 대하여 다루어보자. 만약 $g(\theta)$의 sequence of estimator $\delta_n$이 consistent하다면, $\delta_n - g(\theta)$의 distribution 자체도 $n$이 커질 수록 0에 집중되게 될 것이다. 하지만, convergence in probability는 얼마나 빨리 converge할지, 혹은 $n$이 infinte여도 어떤 특정 값으로의 집중이 아니고 여전히 특정 distribution을 따르는 경우 어떤 distribution으로 converge할지 알려주지 못한다. 그러므로 우리는 새로운 개념의 convergence를 도입해야 하는데, 바로 convergence in distribution_분포수렴이다.

Definition 19.9 Sequence of random variable $Y_n$이 각각 cumulative distribution function(CDF) $H_n$을 가지고 있다고 하자. $Y_n$이 $Y$로 converge in distribution(혹은 converge in law)한다는 것은 $Y$의 CDF $H$에 대하여, $H$가 continuous한 모든 $y$에 대하여

\[H_n(y) \to H(y)\quad \text{as} \quad n\to\infty\]

인 경우이다. 이때 표기는 $Y_n \leadsto Y$ 혹은 $Y_n \leadsto P_Y$로 한다(이 외에도 나타내는 표기가 많은데, 특히 화살표 표기의 경우 $\overset{d}{\to}$, $\overset{\mathcal{L}}{\to}$, $\Rightarrow$ 등이 있다). 이때 $P_Y$는 $Y$의 distribution을 나타내는 probability measure이다.

가장 의심스러운 부분 중 하나는 convergence in distribution이 $H$가 continuous한 곳에서만 point-wise convergence를 만족하면 된다는 점이다. 왜 하필 continuous point에서만일까? 이를 조금 더 자연스럽게 받아들이기 위해 다음 예를 살펴보자.

Example 19.10 $Y_n = 1/n$이라고 하자. 즉, random variable이지만 특정 값에 probability 1로 몰려있는 degenerate한 경우이다. 그리고 random variable $Y$는 항상 0을 준다고 하자. 그러면

\[H_n(y) = P_{Y_n}([-\infty, y])= P(Y_n \le y) = I\{1/n\le y\}\]

만약 $y\gt0$이라고 하면, $1/n$이 언젠가 결국 $y$보다 작아지므로(Archmedean) $n\to\infty$임에 따라 $H_n(y) = I\{1/n\le y\}\to 1$가 된다. 만약 $y\le 0$이면, 모든 $n$에 대하여 $H_n(y) = I\{1/n \le y\}=0$이므로 $n\to\infty$임에 따라 $H_n(y)\to 0$이 된다. 우리는

\[H(y) = P_Y([-\infty, y]) = P(Y\le y) = I\\{0\le y\\}\]

임을 알고 있으므로, $y\ne0$에 대해선 $H_n(y)\to H(y)$를 증명했음을 알 수 있다. 하지만

\[H_n(0) = 0 \to 0\ne 1 = H(0)\]

이므로 성립하지 않는다. $Y_n$과 $Y$를 하나의 숫자로 본다면 $1/n$은 0으로 수렴하므로 $Y_n \leadsto Y$로 결론짓는 것이 훨씬 더 자연스럽다. 하지만, 바로 위 경우와 같이 $y=0$인 경우에서는 CDF가 converge 않는데, 이 점은 알고보면 $H$가 discontinuous한 point이었음을 알 수 있다.

그리고 CDF는 사실 discontinuity point를 아무리 많이 가져봐야 countable만큼만 가진다. 그 이유를 간단하게 알아보자. 어떤 random variable $X$의 CDF $F$에 대하여 $A_n:=\{y: P(X = y)\gt 1/n\}$이라고 두자. 그러면 point probability가 $1/n$보다 큰 point가 $n$개 이상 있으면 전체 probability는 1을 넘어가므로 $\vert A_n \vert \lt n$이다. 또, $F$의 discontinuity point들의 전체 집합은 $A_n$의 union이므로, 결국 우리는 discontinuity point들의 전체 집합은 countable set임을 알 수 있다.

그러므로 continuous point에서만 convergent 조건이 성립해도 CDF는 a.e. pointwise convergence를 만족하는 격이 된다.

Convergence in distribution을 정의함으로써 우리는 estimator의 limiting distribution을 알 수 있게 된다. 더 구체적으로는 estimator 그 자체의 limiting distribution은 아닐 수 있지만, 그 estimator가 0으로 converge하거나 diverge하지 않을 $n$에 관한 식을 적절히 곱한 estimator에 대해서는 limitiing distribution을 알 수 있다는 것이 큰 장점이다. 이는 이후에 충분히 큰 $n$에 대해서 근사치를 제공하고 estimator의 경향성 등을 파악하며, 얼마나 빠른 속도로 특정 distribution에 converge하는지도 알려주어 performance에 대한 정보도 함께 얻을 수 있다.

Example 19.11 $X_1, X_2, \cdots$가 density

\[f\_{\theta}(x) = \begin{cases} (x - \theta)e^{-(x-\theta)} & x\ge\theta \\ 0 & \text{otherwise}\\ \end{cases}\]

를 가지는 distribution으로부터 추출된 i.i.d. sample이라고 하자. 또한, $M_n:= \min\{X_1, \cdots, X_n\}$으로 둘 때, $M_n$은 $\theta$에 대한 consistent한 estimator임을 먼저 보일 것이다.

먼저 $M_n$의 CDF와 관련된 수치들을 먼저 알아보도록 하자.

\[P(M_n\ge t) = P(X_i \ge t,\,\forall i) = (t-\theta+1)^ne^{-n(t-\theta)}, \quad t\ge \theta\]

이고 나머지 $t$에 대해서는 0이다. Consistency의 정의에 따라

\[\begin{align*} P_{\theta}(\vert M_n - \theta\vert \gt\epsilon) &= P_{\theta}\left(M_n\ge\frac{t}{\sqrt{n}}+\theta\right) \\ &= P_{\theta} (\theta+\epsilon\lt M_n) + 1 - P_{\theta}(\theta-\epsilon\le M_n)\\ &= (\epsilon+1)^ne^{-n\epsilon} + 1 - 1 \\ &\to 0 \quad \text{as}\quad n\to\infty \end{align*}\]

이므로 consistent함을 알 수 있다. 이제 limiting distribution을 찾을 것인데, 어느 속도로 converge하는지 아직 모르므로 어떤 $\alpha$에 대하여 $n^{\alpha}(M_n - \theta)$의 limiting distribution을 고려해보도록 하자. 원래 CDF를 고려해야하지만, $M_n$이 정의된 특성상 1- CDF를 고려하는 것이 계산상 편리하다. $t\ge0$에 대하여

\[\begin{align*} P_{\theta}(n^{\alpha}(M_n - \theta)\ge t) &= P_{\theta}\left(M_n\ge \frac{t}{n^{\alpha}}+\theta\right) \\ &= \left(tn^{-\alpha} + 1\right)^n e^{-tn^{1-\alpha}} \end{align*}\]

0이 아닌 극한값이 존재할 적절한 $\alpha$와 그 극한값을 알기 위해서 log를 씌운 후 Taylor expansion을 해보자.

\[\begin{align*} \log P_{\theta}(n^{\alpha}(M_n - \theta)\ge t) &= -tn^{1-\alpha}+n\log(1+n^{-\alpha}) \\ &= -tn^{1-\alpha} + n\left(nt^{-\alpha} - \frac{1}{2}t^2n^{-2\alpha} + \frac{1}{3}t^3n^{-3\alpha}-\cdots\right) \\ &= -\frac{1}{2}t^2 n^{1-2\alpha} + \frac{1}{3}t^3n^{1-3\alpha} - \cdots \\ \end{align*}\]

그러므로 적절한 $\alpha = 1/2$이며, 극한값은 $e^{-t^2/2}$임을 알 수 있다. 따라서

\[\sqrt{n}(M_n - \theta)\leadsto Y\]

이며, 이때 $Y$의 CDF는

\[F_Y(y) = \begin{cases} 1 - e^{-t^2/2} & t\ge 0 \\ 0 & \text{otherwise} \\ \end{cases}\]

이다. 이는 Weibull distribution의 일종이 가지는 CDF다.

Theorem 19.12 Convergence in distribution $Y_n \leadsto Y$가 성립하는 것과, 모든 bounded continuous function $f$에 대하여

\[E^*f(Y_n) \to Ef(Y) \quad \text{as}\quad n\to\infty\]

가 성립하는 것은 equivalent하다. 이때 $E^*$는 $f(X_n)$을 dominate하는 가장 작은 probability measure에 대한 expectation이다.

위의 성질을 만족하는 convergence를 weak convergence라고 부른다. 이 정의는 convergence in distribution을 단순히 random variable에서뿐만 아니라 random vector, 혹은 measurable하지도 않는 random variable, random function 등의 매우 일반적인 metric space에서 정의되는 random variable에 대해서도 확장하는데 매우 큰 도움을 준다.

Corollary 19.13 만약 $g$가 continuous function이고 $Y_n\leadsto Y$일 때,

\[g(Y_n) \leadsto g(Y)\]

가 성립한다.

Proof: 만약 $f$가 bounded하고 continuous하다면, $f\circ g$도 bounded하고 continuous하다. $Y_n\leadsto Y$인 것과

\[Ef(g(Y_n)) \to Ef(g(Y))\]

인 것이 Theorem 19.12에 의하여 equivalent하다. 이를 다시 $f$의 시각으로만 보면, $g(Y_n)$의 $g(Y)$으로의 convergence in distribution이 성립한다.

이제 매우 중요한 theorem 하나를 살펴볼 예정이다. 이는 convergence in distribution에서 가장 기본이 되는 틀인데, 이 theorem은 앞으로 convergence in distriution을 살펴볼 때 converge하는 distribution의 기본 틀을 제공해준다.

Theorem 19.14 (Central Limit Theorem, CLT_{중심극한정리}) Mean $\mu$와 variance $\sigma^2$를 가진 population으로투터 i.i.d.한 sample $X_1, X_2, \cdots$를 추출했다고 하자. Sample mean $\overline{X}_n = (X_1+\cdots+X_n)/n$이라고 하면, 다음이 성립한다.

\[\sqrt{n}(\overline{X}\_n - \mu)\leadsto N(0, \sigma^2) \quad \text{as}\quad n\to\infty\]

CLT의 증명은 다음 편에서 characteristic function_{특성 함수}의 도입과 함께 알아보도록 하겠다. CLT가 제공해주는 정보는 weak law of large numbers(WLLN)보다 더 많음을 알 수 있다. Sample mean $\overline{X}_n$이 단순히 한 점으로 converge하는 정보를 주는 WLLN과 는 달리, CLT는 sample mean이 $1/\sqrt{n}$의 속도로 normal distribution으로 converge함을 알려주기 때문이다. CLT는 단언코 통계학에서 가장 활용도가 높고 매우 주요한 성질을 담고 있다. CLT는 단지 i.i.d. random sample에서만 적용되는 것은 아니고, sample끼리 약한 correlation을 띄고 있거나 sample이 서로 다른 distribution으로부터 추출된 경우 등으로 확장이 충분히 가능하다. 또한, 특정 random variable이 $n\to\infty$인 경우에 sample mean과의 차이가 없어짐을 보임으로써 그 random variable도 $1/\sqrt{n}$의 속도로 normal distribution으로 converge(혹은 나아가 normal distribution으로 얼마든지 근사 가능한)함을 보일 수 있다. 이후에 sample mean과 normal distribution은 어느 정도 오차 범위 내에서 근사가 가능한지, 오차의 bound가 연구되기도 하였는데 Berry-Esseen theorem이 이와 관련하여 잘 알려진 theorem 중 하나다. 이는 다음 inequality가 성립함을 보여준다. 이때 $\Phi$는 normal distribution의 CDF이다.

\[\vert P(\sqrt{n}(\overline{X}_n - \mu)\le x) - \Phi(x/\sigma)\vert \le \frac{3E\vert X_1 - \mu\vert^3}{\sigma^3\sqrt{n}}\]

다음은 convergence in probability와 convergence in distribution의 관계에 관한 성질을 보여준다. 이는 정말로 많이 활용되기에 꼭 기억하고, 생각보다 convergence in probability와 convergence in distribution이 상식 외로 성립하지 않는 관계가 있는데 아래 성질은 그래도 성립함을 알고 있으면 도움이 된다.

Theorem 19.15 만약 $Y_n \leadsto Y$, $A_n\overset{p}{\to}$, $B_n\overset{p}{\to}b$가 성립할 때,

\[A_n + B_nY+n \to a+bY\]

를 만족한다.

Proof: 편의상 $A_n\overset{p}{\to} 1$이고 $Y_n\leadsto Y$이면 $A_nY_n\leadsto Y$가 성립함을 증명할 것이다. $F_Y$를 $Y$의 CDF라고 하고, $y$에서 continuous하다고 하자. 그리고 $y+\epsilon$에서도 continuous한 임의의 $\epsilon$에 대하여

\[\begin{align*} \{A_nY_n \le y\}&\subset \{Y_n\le y+\epsilon\}\cup\{A_n\le\frac{y}{y+\epsilon}\} \\ P(A_nY_n \le y)&= P(A_n \le y+\epsilon) + P(Y_n\le\frac{y}{y+\epsilon}) \\ &= P(A_n \le y+\epsilon) + P(\vert A_n - 1\vert\gt\frac{1}{y+\epsilon})\\ &\to P(Y\le y+\epsilon) + 0 = F_Y(y+\epsilon) \end{align*}\]

임에 따라

\[\limsup P(A_nY_n\le y) \le F(y+\epsilon)\]

가 성립한다. 비록 이 inequality가 $F_Y$가 $y+\epsilon$에서 continuous한 $\epsilon$에 대해서 성립하지만, CDF는 거의 모든 곳에서 continuous함을 앞에서 보인 바 있으므로 충분히 작게 잡을 수 있다. 그러므로

\[\limsup P(A_nY_n\le y) \le F(y)\]

이제 $F_Y$가 $y - \epsilon$에서 continuous하고 $y - \epsilon>0$인 $\epsilon$에 대하여 위와 비슷한 과정을 거치면

\[\liminf P(A_nY_n\le y) \ge F(y)\]

가 성립한다. 따라서 $P(A_nY_n\le y)$의 극한이 존재하고 그 극한값이 $F_Y(y)$이므로 $A_nY_n \leadsto Y$가 성립한다.

CLT는 sample mean $\overline{X}_n$에 대한 정보는 충분히 제공하지만, 모든 estimator가 항상 sample mean과 같은 것은 아니다. 이러한 이유로 임의의 estimator에 대해서도 CLT와 비슷한 성질처럼 나타낼 수 있도록 도와주는 theorem이 하나 있다. 이는 Taylor series_{테일러급수}를 활용하여 임의의 estimator를 sample mean에 관하여 근사된 식으로 나타낼 수 있다.

Proposition 19.16 (Delta Method) CLT(Theorem 19.12)에서 언급한 condition들 아래에서, $f$가 $\mu$에서 continuous하고 differentiable하다고 하자. 그러면

\[\sqrt{n}(f(\overline{X}_n) - f(\mu))\leadsto N(0, [f'(\mu)]^2\sigma^2)\]

Proof: $f$가 continuous한 도함수를 가지고 있다고 하자(위에서 언급한 조건대로 증명하려면 조금 더 엄밀성이 필요하나 이는 big O notation을 다룬 후 간단하게 다루어보겠다). 그러면 Taylor expansion에 따라

\[f(\overline{X}_n) = f(\mu) + f'(\mu_n)(\overline{X}_n - \mu)\]

를 만족하는 $\mu_n$이 $\overline{X}_n$과 $\mu$ 사이에 존재한다. $\vert \mu_n - \mu\vert\le \vert\overline{X}_n -\mu\vert$ 임에 따라 $\overline{X}_n\overset{p}{\to} \mu$이어서 $\mu_n\overset{p}{\to}\mu$가 성립한다. 또한 $f’$이 continuous하므로 $f’(\mu_n) \overset{p}{\to} f’(\mu)$가 Proposition 19.5에 의해 성립한다. 따라서 $Z = N(0, \sigma^2)$라고 하면 Theorem 19.15에 의하여

\[\sqrt{n}(f(\overline{X}_n - f(\mu))) = f'(\mu_n)[\sqrt{n}(\overline{X}_n - \mu)] \leadsto f'(\mu)Z \sim N(0, [f'(\mu)]^2\sigma^2)\]

이다.

Delta method의 쓰임을 알아보기 위해 다음 예시를 살펴보자.

Example 19.17 Uniform distribution $\mathcal{U}(1, 2)$에서 추출된 i.i.d. random sample $X_1, X_2, \cdots$에 대하여 harmonic sample mean

\[H_n:= \frac{n}{X_1^{-1}+\cdots +X_n^{-1}}\]

을 고려하자. 먼저

\[H_n^{-1} = \frac{X_1^{-1} + \cdots +X_n^{-1}}{n}\]

에 대해 고려하도록 하자. $Y_i = \log X_i$를 두면 $H_n^{-1}$은 $Y_i$의 sample mean이다. $Y_i$는 $1/2$과 $1$ 사이의 값을 가진다.

\[EY_i = \int_1^2 \frac{1}{x}\cdot1\,dx = [\log{x}]_1^2 = \log 2\]

이므로 WLLN(weak law of large numbers)에 의하여

\[H_n^{-1} \overset{p}{\to} \log{2}\]

이다. $f(x) = 1/x\, (1/2\le x\le 1)$으로 두면 $f$는 continuous하고 bounded하므로

\[H_n \overset{p}{\to} \frac{1}{\log 2}\]

이다.

이제 limiting distribution를 구해보도록 하자.

\[\begin{align*} EY_i^2 &= \int_1^2 \frac{1}{x^2}\cdot 1\,dx = \frac{1}{2} \\ Var(Y_i) &= EY_i^2 - (EY_i)^2 = \frac{1}{2} - (\log 2)^2 \end{align*}\]

이므로, CLT에 의하여

\[\sqrt{n}(H_n^{-1} - \log2) \leadsto N\left(0, \frac{1}{2} - (\log 2)^2\right)\]

가 성립한다. $f(x) = 1/x\,(1/2\le x\le 1)$은 $f’(x) = -1/x^2\,(1/2\le x\le 1)$임에 따라 continuously differentiable하므로 Delta method에 의하여

\[\sqrt{n}\left(H_n - \frac{1}{\log2}\right)\leadsto N\left(0, \frac{1/2-(\log2)^2}{(\log2)^4}\right)\]

임을 알 수 있고, 이로써 limiting distribution을 알게 되었다.

위의 Theorem 19.12에서 $X_n\leadsto X$인 것과 bounded하고 continuous한 함수 $f$에 대하여 $Ef(X_n)\to Ef(X)$는 equivalent함을 다루었다. 만약 $f$가 continuous하지만 bounded하지 않으면 이 성질은 만족하지 않을 수 있다. 하지만 아래서 정의되는 uniformly integrable한 성질을 random variable이 가지고 있으면 $f$가 bounded되지 않아도 이러한 성질이 유지됨이 알려져 있다.

Definition 19.18 Random variables $X_n,\, n\ge 1$이 uniformly integrable하다는 것은, $t\to\infty$임에 따라

\[\sup_{n\ge 1} E[\vert X_n\vert I\{\vert X_n\vert \ge t\}] \vert\to 0\]

가 성립하는 것이다.

우리는

\[E\vert X_n \vert = E[\vert X_n\vert I\{\vert X_n\vert\lt t\}] + E[\vert X_n\vert I\{\vert X_n\vert\ge t\}] \le t + E[\vert X_n\vert I\{\vert X_n\vert\ge t\}]\]

임을 알 수 있다. 그러므로 만약 어떤 $t$에 대하여 $\sup_{n\ge 1} E[\vert X_n\vert I{\vert X_n\vert \ge t}]$가 finite하다면, $\sup_n E\vert X_n\vert\lt\infty$가 성립한다. 그러므로 uniform intergrability가 성립하면 $\sup_n \vert X_n\vert\lt\infty$가 성립함을 알 수 있다. 하지만 converse는 성립하지 않는다. 이를테면, $Y_n \sim \text{Ber}(1/n)$이고 $X_n:= Y_n$으로 두면 $E\vert X_n\vert = 1$이 성립하지만 $X_n$은 uniformly integrable하지 않음을 알 수 있다.

Theorem 19.19

• 만약 $X_n\leadsto X$라면,

\[E\vert X\vert \le \liminf E\vert X_n\vert\]

가 성립한다.

• 만약 $X_n,\, n\ge 1$이 uniform integrable하고 $X_n \leadsto X$이면, $EX_n\to EX$가 성립한다.
• 만약 $X$와 $X_n,\, n\ge 1$이 non-negative하고 integrable하다(즉, $E\vert X\vert <\infty$, $E\vert X_n\vert <\infty$)고 하고 $EX_n\to EX$가 성립하면, $X_n,\, n\ge 1$은 uniformly integrable하다.

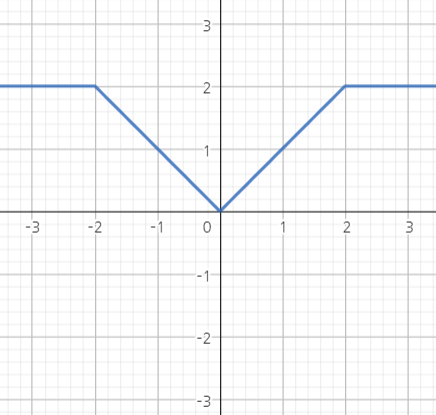
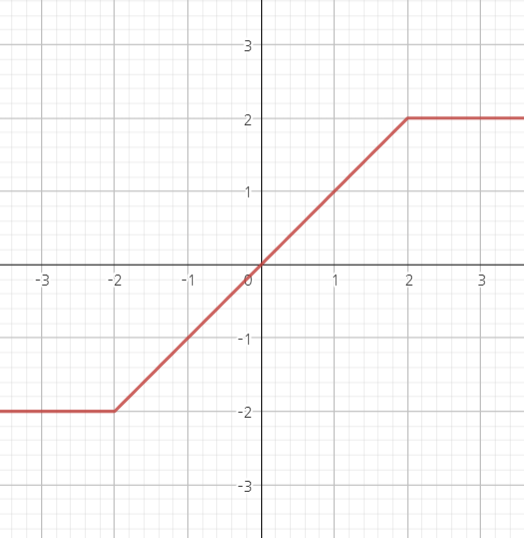
Proof: $x\wedge y := \min{x, y}$이고 $x\vee y := \max{x, y}$라고 기호를 정의할 때 다음 두 함수를 고려하자.

\[g_t(x) = \vert x\vert \wedge t, \quad h_t(x) = -t\vee(x\wedge t)\]

두 함수의 개형은 다음과 같다. 식보단 개형으로 두 함수를 기억하기 바란다. 파란색이 $g_t$, 빨간색이 $h_t$를 나타낸다.

이 함수들은 모두 bounded하고 continuous하다. 그러므로 만약 $X_n\leadsto X$라면, $Eg_t(X_n)\to Eg_t(X)$이고 $Eh_t(X_n)\to Eh_t(X)$가 성립한다.

첫 번째 명제를 먼저 증명해보자.

\[\liminf E\vert X_n \vert \ge\liminf E g_t(X_n) = Eg_t(X) = E\vert X\vert\wedge t\]

가 성립하고, 마지막 term은 monotone convergence에 의하여 $t\to\infty$임에 따라 $E\vert X\vert$로 increasing하며 converge한다.

이제 두 번째 명제를 증명해보자. Uniform regularity와 첫 번째 명제에 의하여

\[E\vert X\vert \le\liminf E\vert X_n\vert \lt \infty\]

가 성립한다. 또한, $\vert X_n - h_t(X)\vert \le \vert X_n\vert I{\vert X_n\vert \ge t}$가 성립하므로 임의의 $t>0$에 대하여

\[\begin{align*} \limsup \vert EX_n - EX\vert &= \limsup\vert (Eh_t(X_n) - Eh_t(X)) + E(h_t(X) - X) + E(X_n - h_t(X_n))\vert \\ &\le \limsup \vert Eh_t(X_n) - Eh_t(X)\vert + E\vert X - h_t(X)\vert + \sup E\vert X_n - h_t(X_n)\vert \\ &\le E\vert X - h_t(X)\vert + \sup E[\vert X_n\vert I\{\vert X_n\vert \ge t\}] \end{align*}\]

가 성립한다. 이때 세 번째 inequality에서는 limsup은 non-increasing하므로 임의의 $m$에 대하여 $\sup_{n\ge m}$의 값이 $\limsup_n$ 값보다 큼이 활용되었고, $,X_n\leadsto X \implies Eh_t(X_n)\to Eh_t(X)$임도 활용되었다. 마지막 항은 monotone convergence와 uniform integrability에 의하여 $t\to\infty$임에 따라 0으로 converge하므로 $\limsup \vert EX_n - EX\vert =0$이다. 따라서 증명되었다.

마지막 명제를 증명해보자. $X$와 $X_n$이 non-negative하고 $EX_n\to EX$이고, $X_n \leadsto X \implies Eg_t(X_n)\to Eg_t(X)$가 성립하므로, 임의의 $t>0$에 대하여

\[E(X_n - t)^+ = EX_n - Eg_t(X_n) \to EX - Eg_t(X) = E(X - t)^+\]

가 성립한다(두 번째 equality는 $X_n - t$의 양수 부분은 $X_n$에서 $X_n$와 $t$ 중 최소인 것을 뺀 거라고 생각하면 쉽다). 그리고 uniform integrability의 정의에서 나오는 $X_n I{X_n \ge t}$는 얼추 $(X - t)^+$로 bound를 잡을 수 있는데, $x\gt 0$에 대하여 $x I{x\ge 2t} \le 2(X - t)^+$로 잡으면 된다. 그러면

\[\limsup E[X_n I\{X_n\ge 2t\}] \le \limsup 2E(X_n - t)^+ = 2E(X - t)^+\]

가 성립한다. Dominated convergence에 의해 $t\to\infty$임에 따라 $E(X - t)^+\to 0$이므로

\[\lim_{t\to\infty} \limsup E[\vert X\_n\vert I\{X_n \ge 2t\}] = 0\]

가 성립한다. 마지막 과정으로 $\limsup_n$이 아닌 $\sup_n$에 대해서도 위의 식이 성립함을 증명하면 된다. 임의의 $\epsilon >0$에 대하여, 먼저 위의 식에 의하여 다음을 만족하는 $t_1 >0$이 존재한다.

\[\limsup_n E[\vert X_n\vert I\{X_n \ge t_1\}] \lt\epsilon\]

다시 동일한 $\epsilon$에 대하여 다음을 만족하는 $N>0$이 존재한다.

\[\sup_{n>N} E[\vert X_n\vert I\{X_n \ge t_1\}] \lt\epsilon\]

$X_n$이 integrable, 즉 $E\vert X_n\vert\lt\infty$이기 때문에 dominated convergence에 의하여 $t\to\infty$임에 따라 $E\vert X_n\vert I\{\vert X_n\vert \ge t\}\to 0$이 성립한다. 그러므로 다음을 만족하는 $t_2$가 존재한다.

\[\sup_{n\le N} E[\vert X_n\vert I\{X_n \ge t_2\}] \lt\epsilon\]

따라서 각 $\epsilon>0$마다 $t_0 = t_1 \vee t_2$로 잡으면

\[\sup_n E[\vert X_n\vert I\{X_n \ge t_0\}]\lt\epsilon\]

가 성립하므로

\[\sup_n E[\vert X_n\vert I\{X_n \ge t_0\}] \to 0 \quad \text{as}\quad t\to\infty\]

임이 증명되었다. 즉, $X_n$은 uniformly integrable하다.